# 数字推理
# 等差数列
- 从第二项起,每一项与它的前一项的差等于同一个常数的一种数列。
# 等比数列
- 从第二项起,每一项与它的前一项的比值等于同一个常数的一种数列。
# 质数数列
质数:指在大于 1 的自然数中,除了 1 和它本身以外不再有其他因数的自然数。
基础质数数列
- 2,3,5,7,11,13,17…
例子
4,5,7,9,13,(15),规律:在质数数列的基础上每项加 2
4,6,10,14,22,(26),规律:在质数数列的基础上每项乘以 2
如何判定
- 如果一个数列相邻两项做差后得到的新数列的变化趋势是上升 -> 不变 -> 上升,那么这个数列就可能跟质数数列有关,此时可以考虑在基础质数数列的基础上通过四则运算进行转换,看看能否得到该数列。
# 合数数列
合数:在大于 1 的整数中除了能被 1 和本身整除外,还能被其他数(0 除外)整除的数。
基础合数数列
- 4,6,8,9,10,12,14,15,16…
注意
0 和 1 既不是质数也不是合数。
2 是质数里面唯一的偶数。
# 简单递推数列
【和】0,1,1,2,3,5,8,13…
【差】20,11,9,2,7,-5,12…
【积】4,1/2,2,1,2,2,4…
【商】54,18,3,6,1/2,12…
# 周期数列
2,1,3,2,1,3…
例子
- 1,2,5,6,9,10,(13),规律:相邻两项做差后得到的新数列是周期数列:1,3,1,3,1,...
# 多重数列
1. 基本特征
数列较长:数列中的项数包括(),一般能达到 8 项或 8 项以上;
两个括号:在某些多重数列中,会含有两个括号,即两个未知项。
2. 解题方法
隔项交叉:找奇偶项是否分别称规律。
两两分组:验证两个数 “除乘减加” 的关系。
三三分组:
一般验证 “两小到一大” 规律,如加法、乘法、乘方、差方、差倍等关系。
也有可能是三项整体求和的规律,不过这种情况非常少。
3. 例子
2,8,4,16,6,32,8,(64),规律:隔项交叉
40,3,35,6,30,9,(25),12,20,(15),规律:两两分组相加
1,2,2,6,3,15,3,21,4,(44),规律:两两分组相除
5,24,6,20,8,15,10,(12),规律:两两分组相乘
1,2,5,3,4,19,5,6,(41),规律:三三分组,1 +
= 5
# 分数数列
前后看:交叉。
上下看:
分子分母是否单独成规律;
通分(分子或分母都可以通分);
看趋势(看分子或分母是递增还是递减,优先考虑递增)。
例子
, , , ,( ),规律:后一项的分子等于前一项的分母,后一项的分母等于前一项的分子加分母。 , , , ,( ),规律:后一项的分子是前一项的分子加分母,后一项的分母等于前一项的分母加后一项的分子。 , , , ,( ),规律:每一项的分子成等差数列,相邻两项的分母做差后是合数数列。 ,( ), , , ,规律:直接通分分母。 , , , , ,( ),规律:看分子分母趋势,分子的趋势是递增 2 倍,分母的趋势是递减 3。 , , , , , ,( ),规律:看分母趋势,优先考虑递增,将最后一项的分子分母乘以 2,就可以看出规律了。
# 幂次数列
📌 1. 30 以内数的平方
1、4、9、16、25、36、49、64、81、100 、121、144 、169、196 、225 、256 、289 、324、361、400、441、484、529、576、625、676、729、784、841、900
📌 2. 10 以内数的立方
1、8、27、64、125、216、343、512、729、1000
📌 3. 2、3、4、5、6 的多次方
2 的 1-10 次幂:2、4、8、16、32、64、128、256、512、1024
3 的 1-6 次幂:3、9、27、81、243、729
4 的 1-5 次幂:4、16、64、256、1024
5 的 1-5 次幂:5、25、125、625、3125
6 的 1-5 次幂:6、36、216、1296、7776
熟记
📌 4. 关于常数 0 和 1
,0 是 0 的任意自然数次方(0 的 0 次方没有意义!即此处 N 0); (a 0); 1 是任意非零数的 0 次方,是 1 的任意次方,是 -1 的任意偶次方。
📌 5. 关于单位分数(分母是整数,分子是 1 的分数)
(a 0),例如: ; ,例如: 。
📌 6. 幂次数列做题原则
先确定幂指数形式单一的数值(除了 1、16、64、81 之外的数值)。
如果底数和指数都不一样,先确定底数规律。
注意
如果不是常规形式的幂次数列(
例子
16,36,64,81,100,(144),规律:合数数列的平方
1,32,81,64,25,(6),1,规律:
27,16,5,(1),
,规律: 3,8,24,48,120,(168),规律:幂次修正数列
# 多级数列
- 解题思路
例子
42,40,37,32,25,(14),1,规律:前一项减后一项,做差后得到的新数列是质数数列
10,12,15,20,27,(38),规律:后一项减前一项,做差后得到的新数列是质数数列
0,1,3,9,33,(153),规律:后一项减前一项,做差后得到的新数列可以看作一个新的多级数列,再进行做商,后一项除以前一项,就可以看出规律了
1,2,3,4,7,6,(11),规律:相邻两项做和,得到的新数列是质数数列
-4,4,8,40,(320),规律:后一项除以前一项,得到的新数列是公差为 3 的等差数列
# 递推数列
解题思路
- 优先考虑三项关系,一般找 “两小到一大” 的规律:和、积倍、幂次。如果不通,再考虑两项关系和四项关系。
注意
递推数列分组的时候每组之间有交叉,多重数列分组的时候每组之间没交叉。
例子
23,34,58,93,152,(246),规律:
按多级数列的思路,后一项减前一项可得一个递推和数列:11,24,35,59,前两项之和等于第三项,因此原数列的最后一项与倒数第二项应该相差 94,所以最后一项为 152 + 94 = 246。
按递推数列的思路,分为(23,34,58)、(34,58,93)、(58、93、152),会发现 23 + 34 + 1 = 58、34 + 58 + 1 = 93、58 + 93 + 1 = 152,所以最后一项应该为 93 + 152 + 1 = 246。
118,80,36,42,(-8),规律:分为(118,80,36)、(80,36,42),会发现 118 = 80 + 36 + 2、80 = 36 + 42 + 2,所以有:36 = 42 + 最后一项 + 2,可得最后一项为 -8。
2,4,6,9,13,19,(28),规律:分为(2,4,6)、(4,6,9)、(6,9,13)、(9,13,19),会发现 2 + 4 - 0 = 6、4 + 6 - 1 = 9、6 + 9 - 2 = 13、9 + 13 - 3 = 19,所以最后一项 = 13 + 19 - 4 = 28。
3,7,16,107,(1707),规律:同样三项为一组,会发现 3
7 - 5 = 16、7 16 - 5 = 107,所以最后一项 = 16 107 - 5 = 1707。
# 特殊数列
题目特征:数字较大、整体变化无规律
解题思路:数字拆分找运算规律,最简单的就是 “拆分求和”
例子
2246,3164,5180,6215,(5711),规律:每项拆分求和后都是 14
21,59,1117,2325,(4733),9541,规律:每项拆分成两半之后,找组间的规律
9654, 4832, 5945, 7642, 7963, 8216,(9436),规律:每项拆分成两半之后,找组内的规律
12345,6234,1023,(402),60,规律:每项的首尾之和作为下一项的前面部分,然后剩下的部分照抄
# 小数数列
- 解题思路:把整数部分、小数部分看成 2 个独立的数列推测规律或者看成多级数列来推测规律。
# 根号数列
解题思路:
所有数字变成
的形式。 把根号看成分隔符。
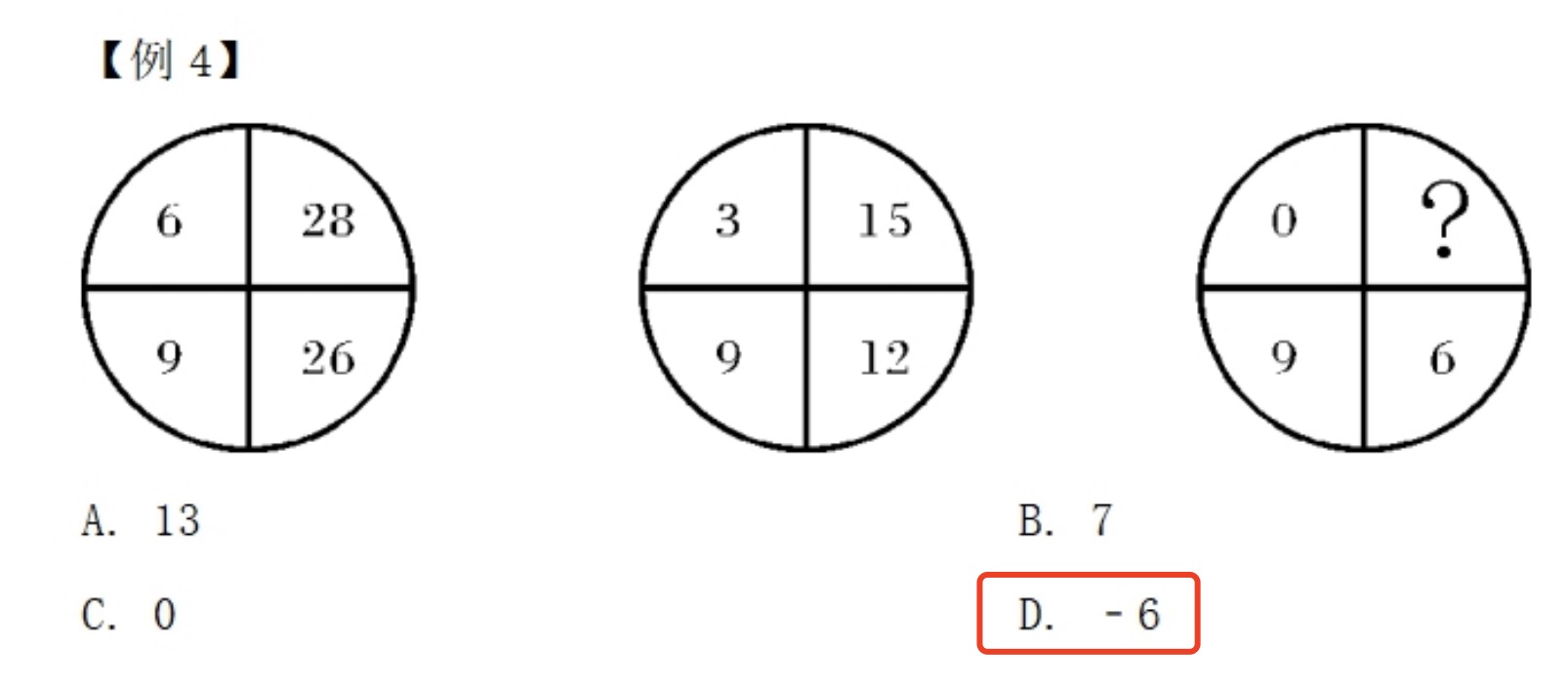
# 图形数阵
1. 无中心
整体求和;
上下左右对角线找等量关系。
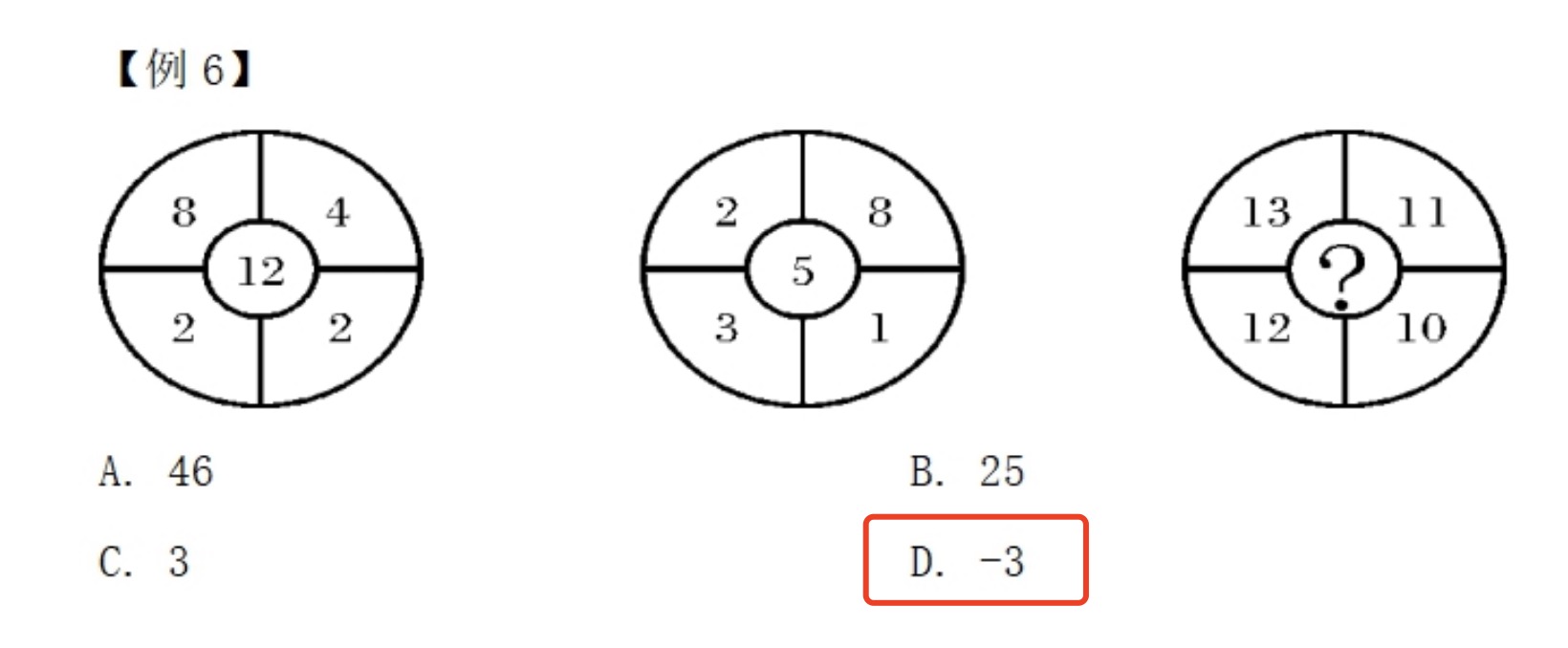
2. 有中心
中心数与四周数有平方关系;
对中心数进行因式分解。
3. 例子
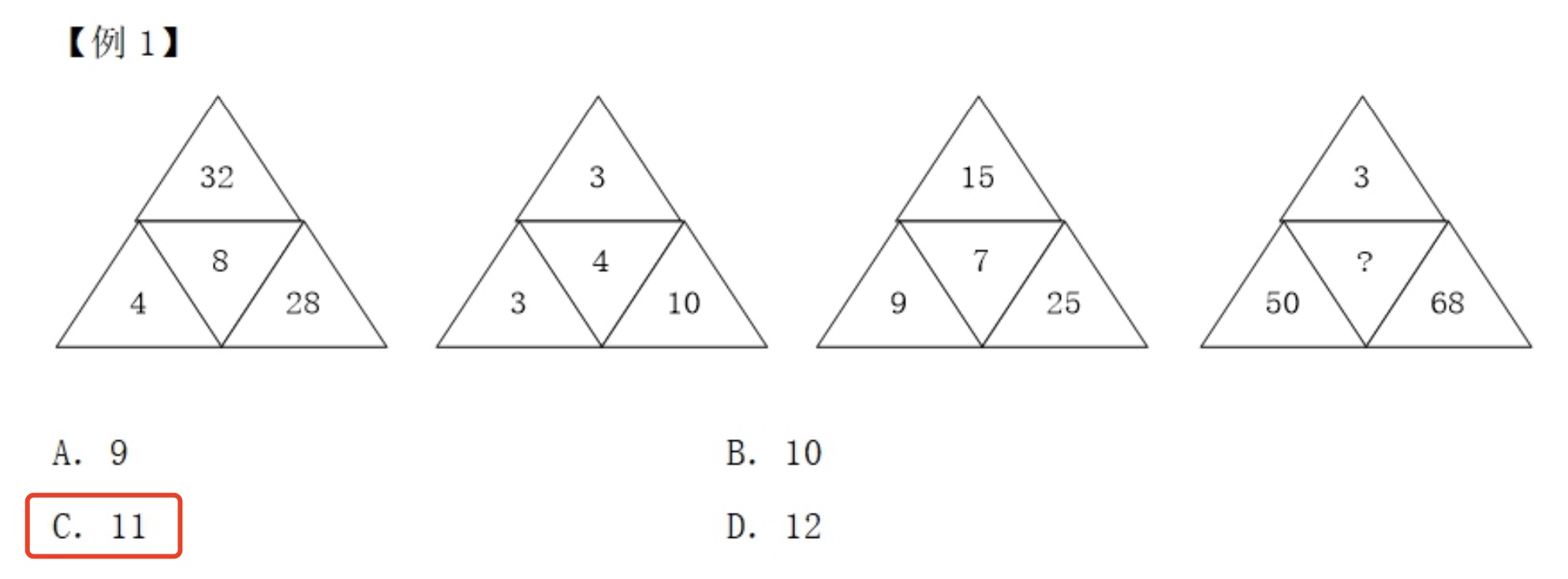
规律:周围数的和刚好是中间数的平方。
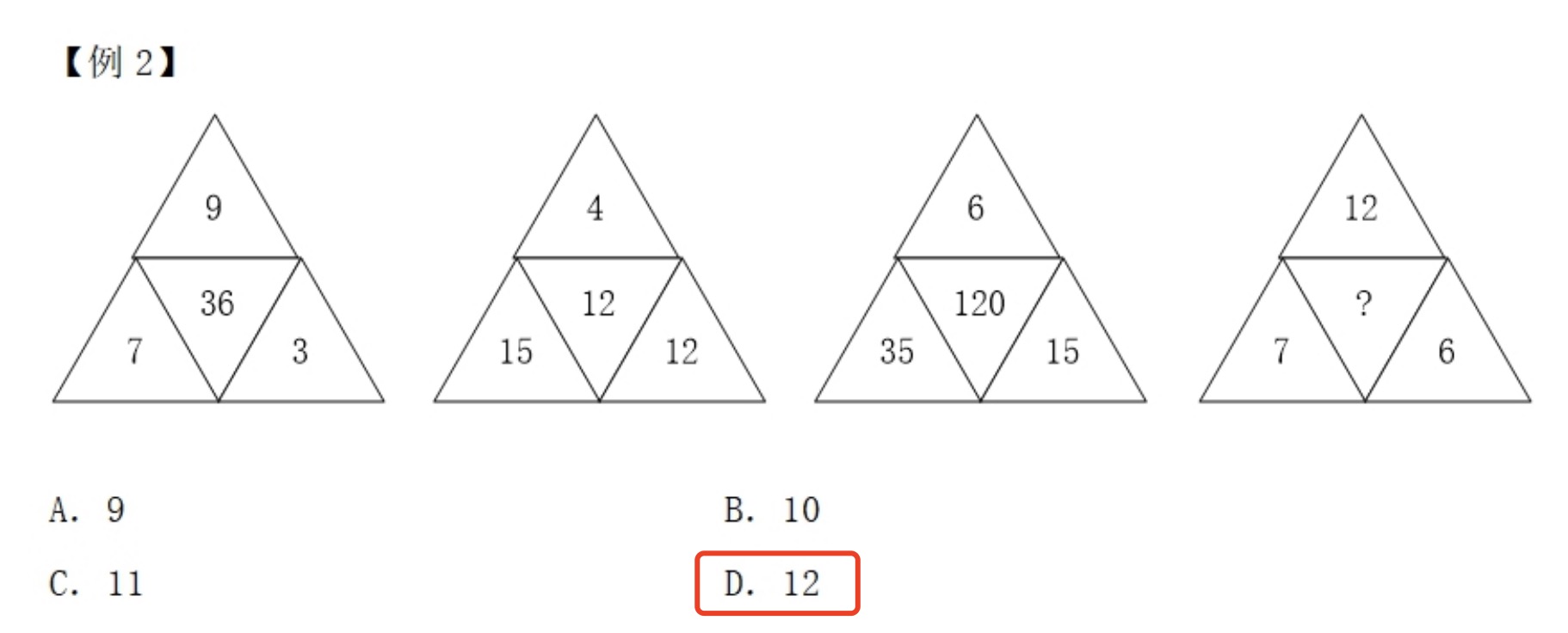
规律:中间数进行因式分解,36 = 4
规律:整体求和都是 50。
规律:左边两个数相乘等于右边两个数相加。
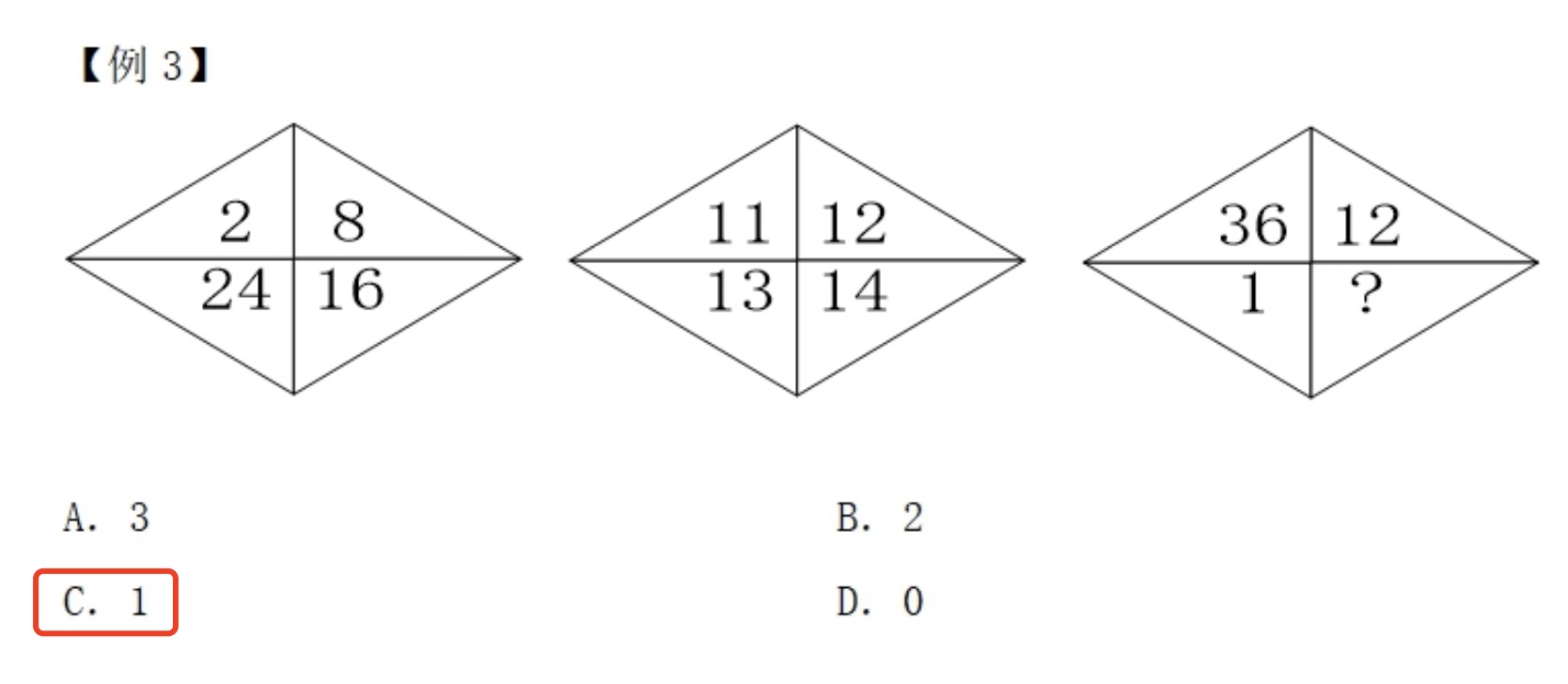
规律:对角线两个数做差相乘就等于中间数,注意做差是有顺序的。
# 矩阵
解题思路:
横纵向整体求和。
横纵向 “两小到一大” 找规律。
# 基础方法
# 代入排除法
常用题型:多位数问题、年龄问题、余数问题、不定方程、选项信息充分。
多位数问题:n 位数,位数之间进行调换或者移动。
年龄问题:核心是年龄差不变。
余数问题:“多(少)几个”、“不足(剩)几个”。
不定方程:未知数的个数大于方程的个数。
选项信息充分:每个选项有两个数据及以上。
# 倍数特性法
整除型
- 题干关键词:“平均”、“每”、“倍“。
余数型
题干关键词:“多(少)几个”、“不足(剩)几个”。
余同取余:用一个数除以几个不同的数,得到的余数相同,此时反求这个数。例:“一个数除以 4 余 1,除以 5 余 1,除以 6 余 1”,这个数可表示为 60n+1。
和同加和:用一个数除以几个不同的数,得到的余数,与除数的和相同,此时反求这个数。例:“一个数除以 4 余 3,除以 5 余 2,除以 6 余 1”,这个数可表示为 60n+7。
差同减差:用一个数除以几个不同的数,得到的余数,与除数的差相同,此时反求这个数。例:“一个数除以 4 余 1,除以 5 余 2,除以 6 余 3”,这个数可表示为 60n-3。
比例型
- 题干关键词:出现比例、分数、百分数。
# 方程法
不定方程
代入排除
- 代入原则:最值代入。问最多(大),先代入最大值;问最少(小),先代入最小值。
奇偶性
奇数×奇数=奇数,奇数×偶数=偶数,偶数×偶数=偶数
奇数±偶数=奇数,奇数±奇数=偶数,偶数±偶数=偶数
和差同性,奇反偶同
倍数特性
假设有一个方程:ax + by = c,如果该方程中任意两部分有共同的最大公约数,则剩下的那部分也应该有这个公约数,此时就可以利用这个倍数特性进行求解问题。
比如:4x + 6y = 64(x、y 都是正整数),其中 4x 和 64 都是 4 的倍数,那么 6y 也应该是 4 的倍数,又因为 6 不是 4 的倍数,那么 y 应该是 4 的倍数,此时将 y 从小往大进行取值,当 y = 4 时,可得 x = 10。因此, y = 4,x = 10 就是该方程的解。
尾数特性
当方程中出现 5x、10x 这样的部分时,就可以考虑用尾数特性的方法进行求解。因为 5x 的尾数只能是 0 或 5,而 10x 的尾数只能是 0。
比如:5x + 4y = 23(x、y 都是正整数),其中 5x 的尾数只能是 0 或 5,假设是 5 的话,因为 23 的尾数是 3,因此 4y 的尾数就是 8(5 + 8 = 13),从而可以推出 y 的尾数是 2,从小往大对 y 进行取值,当 y = 2 时,可求得 x = 5,满足要求,即为解。
不定方程组
消元法
- 消去无关变量变成不定方程求解。
赋 0 法
- 求未知数整体的代数和。
# 赋值法
两种适用情况:
题干中没有任何具体值,只给到了比例倍数关系等(优先赋值不变量)。
找到等量关系满足 “
”,且最多已知一类量。
# 等差数列
通项公式
求和公式
中位数 项数
# 等比数列
通项公式
求和公式
# 平方差公式
# 完全平方公式
# 工程问题
# 赋值总工型(给完工时间型)
1. 题型特征:给出同一工程的多个时间值,即题干有若干个完工时间。
2. 解题思路:赋值总工为时间的最小公倍数,再分别求出各自的效率,最后根据题意列方程。
# 赋值效率型(给效率比例型)
1. 题型特征:
① 题干出现效率比值。
② 题干有若干个相同元素(工人、机器等)。
2. 解题思路:
① 根据比例关系给效率赋值,再根据题意列方程。
② 默认单位效率为 1,赋值元素数量为效率,再根据题意列方程。
注意
这是两种题型特征,分别对应两种解题思路。
拓展
总工 = 效率
时间 总工一定时,时间和效率成反比
工程问题都可以抓住工作总量不变这一点进行列方程。
# 牛吃草型
1. 题型特征:10 头牛 20 天吃完;15 头牛 10 天吃完,则 20 头牛多少天吃完?
2. 解题公式:现有草量 = Y;天数 = T;牛的数量 = N;每天长草量 = X,则 Y = (N × 1 - X) × T
(默认每头牛的效率为 1,则牛的数量 = 牛吃草的速度)
# 行程问题
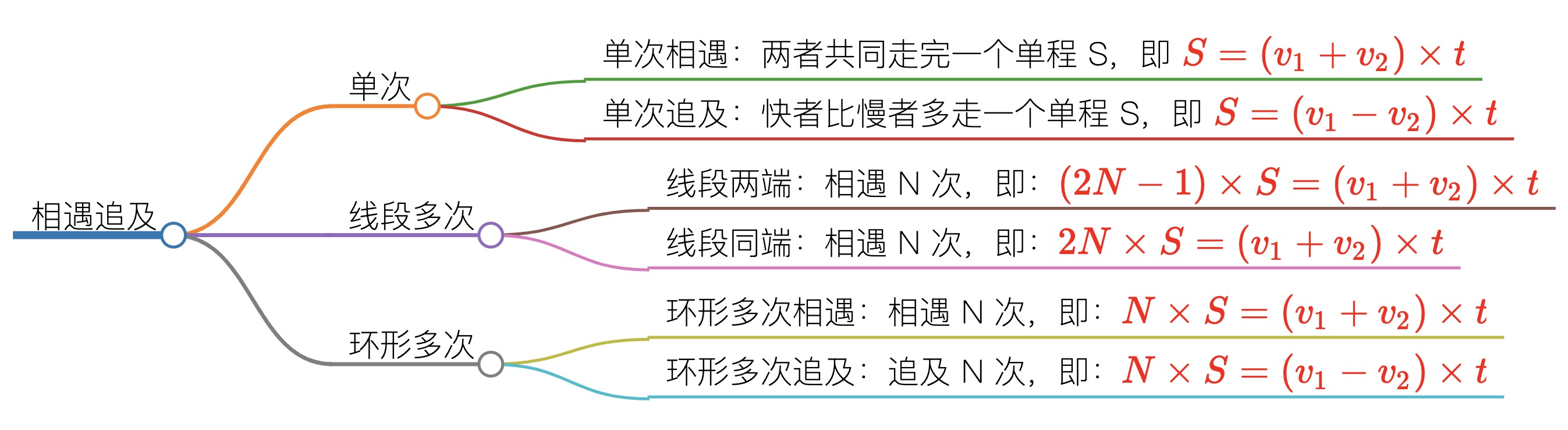
# 相遇追及
注意
做行程问题的时候,要特别注意单位。
当我们根据关系列出方程后,如果想秒,可以根据选项和方程的倍数特性来秒,此时优先考虑 3、7、9 的倍数。
线段多次的问题指的就是在两端之间做往返运动的问题,了解即可,考的特别少。
# 比例行程
路程一定,时间和速度成反比;
时间一定,路程和速度成正比;
速度一定,路程和时间成正比。
# 流水行船
名词释义
# 火车过桥
火车完全通过桥身:行驶的路程 = 桥长 + 车长
整列火车完全在桥上:行驶的路程 = 桥长 - 车长
# 平均速度
S 一定时,平均速度 =
t 一定时,平均速度 =
结论:总路程一定时,等时间的平均速度快于等路程的平均速度。
注意
如果是有平路和上下坡路并且要求全程往返的平均速度的题型,可以秒,直接选平路的速度。
# 经济利润问题
# 核心公式
进价 = 成本
期望利润 = 定价 - 成本,实际利润 = 售价 - 成本
利润率 = 利润 ÷ 成本 = (售价 - 成本) ÷ 成本 = 售价 ÷ 成本 - 1
售价 = 定价 × 折扣,折扣 = 售价 ÷ 定价(“二折” 即售价为定价的 20%)
总售价 = 单价 × 销售量,总利润 = 单件利润 × 销售量
# 基础经济问题
题型特征:计算商品利润、总价、折扣、利润率等。
常用方法:方程法、赋值法(先赋值数量和成本,然后缺啥再设啥)。
# 分段收费
题型特征:超出某个标准按照其他价格计算。
解题方法:找到分段标准,分段计算。
# 函数最值
题型特征:价格每下降 a 元,销量可增加 b 件,求最大利润、收入等。
解题方法:
两点式:二次函数
(a ≠ 0),与 x 轴的交点坐标 ,则当 时,x 取极值。 一般式:二次函数
(a ≠ 0),当 a > 0 时,抛物线开口向上,此时有最小值;当 a < 0 时,抛物线开口向下,此时有最大值;当 时,y 取最值。
注意
这类问题在列方程的时候,如果要求总收入,就用总收入 = 单价
# 最值问题
# 最不利构造
题型特征:至少......保证......
解题方法:最不利情况数 + 1
# 数列构造
题型特征:排名第 N 的至多/少......
解题方法:设未知数 → 构造数列 → 列方程
# 多集合反向构造
题型特征:都......至少......
解题方法:反向 → 求和 → 做差
# 几何问题
# 平面几何
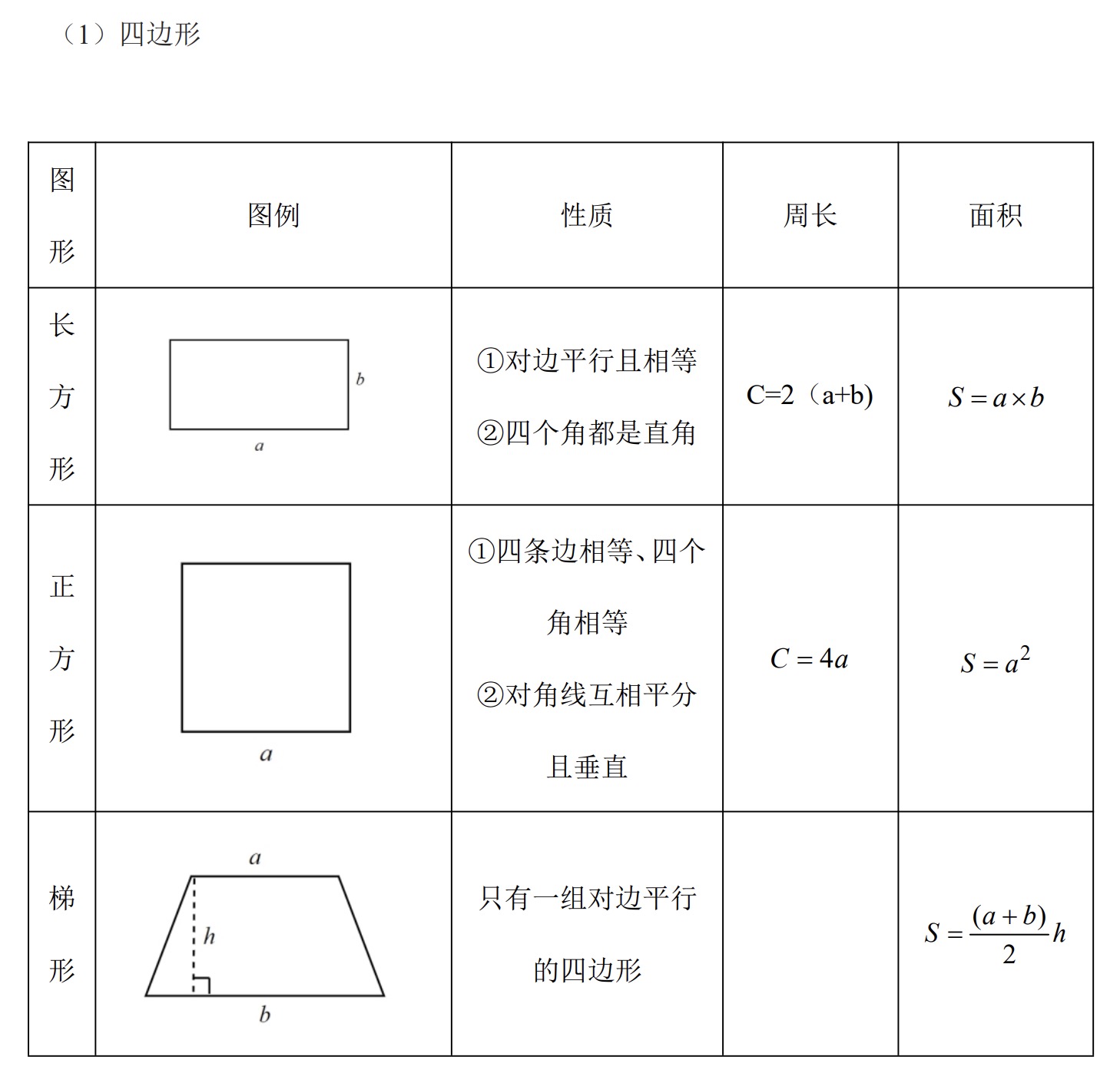
常考题型:平面图形的周长和面积
解题思路:
规则图形运用公式和性质直接求得;
不规则图形则通过割补、平移将其转化为规则图形后,再进行求解。
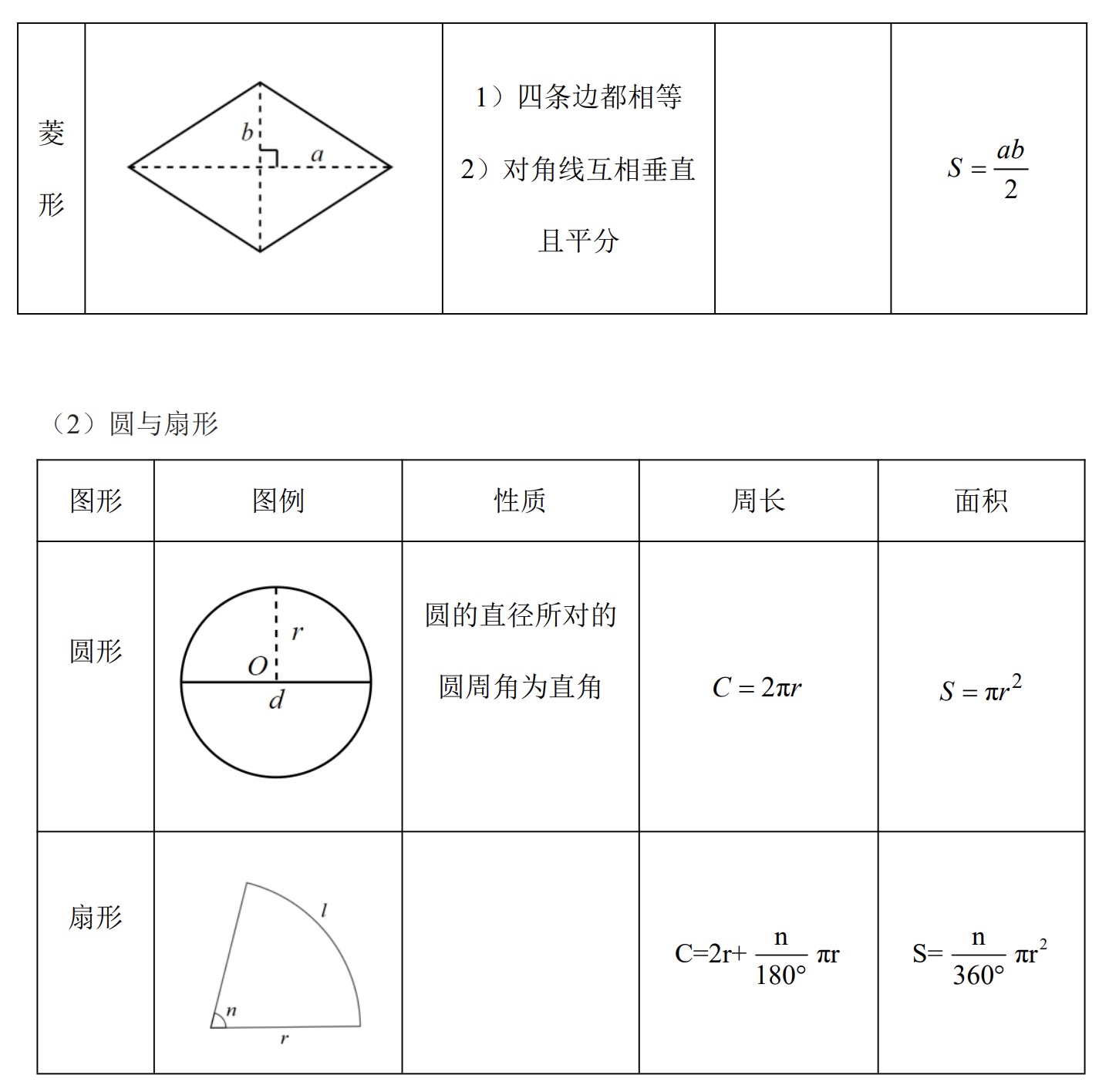
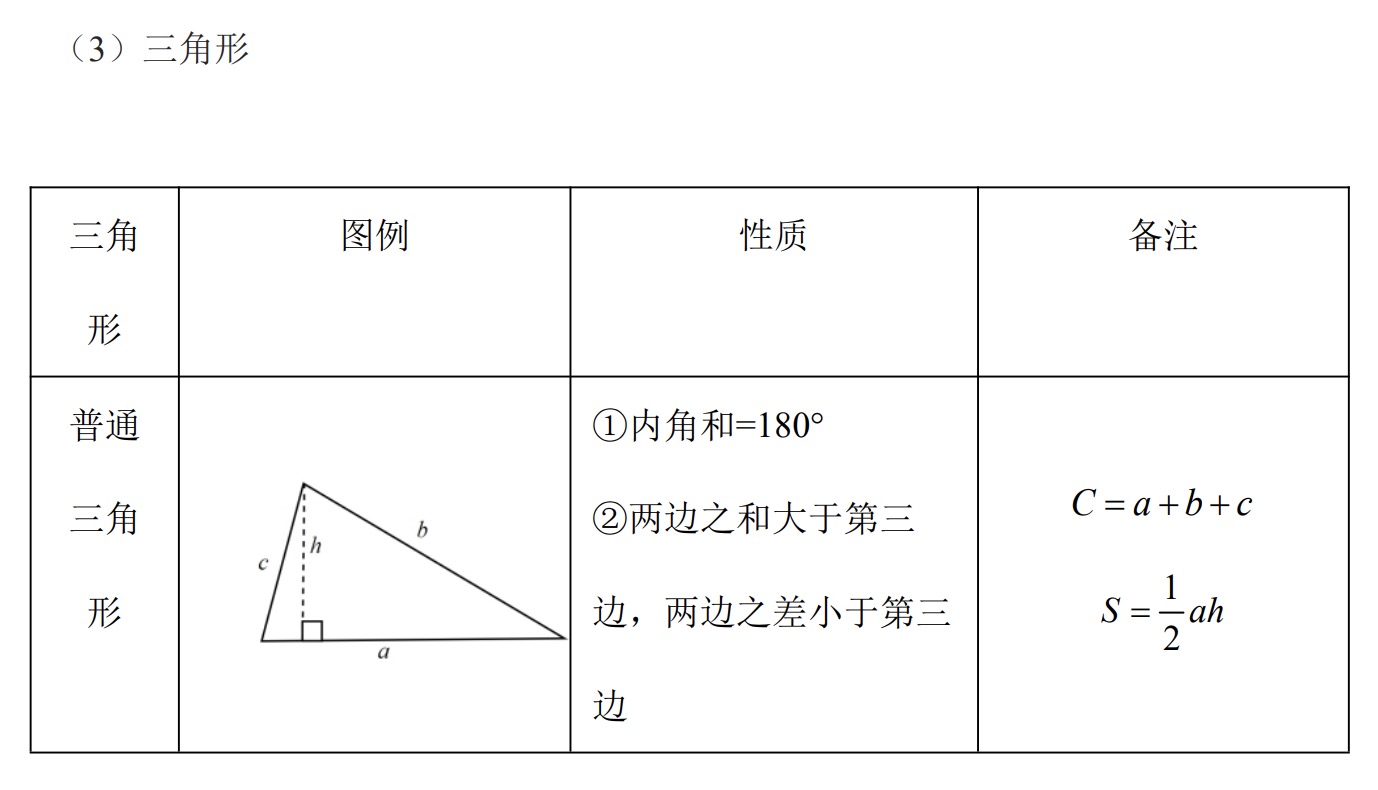
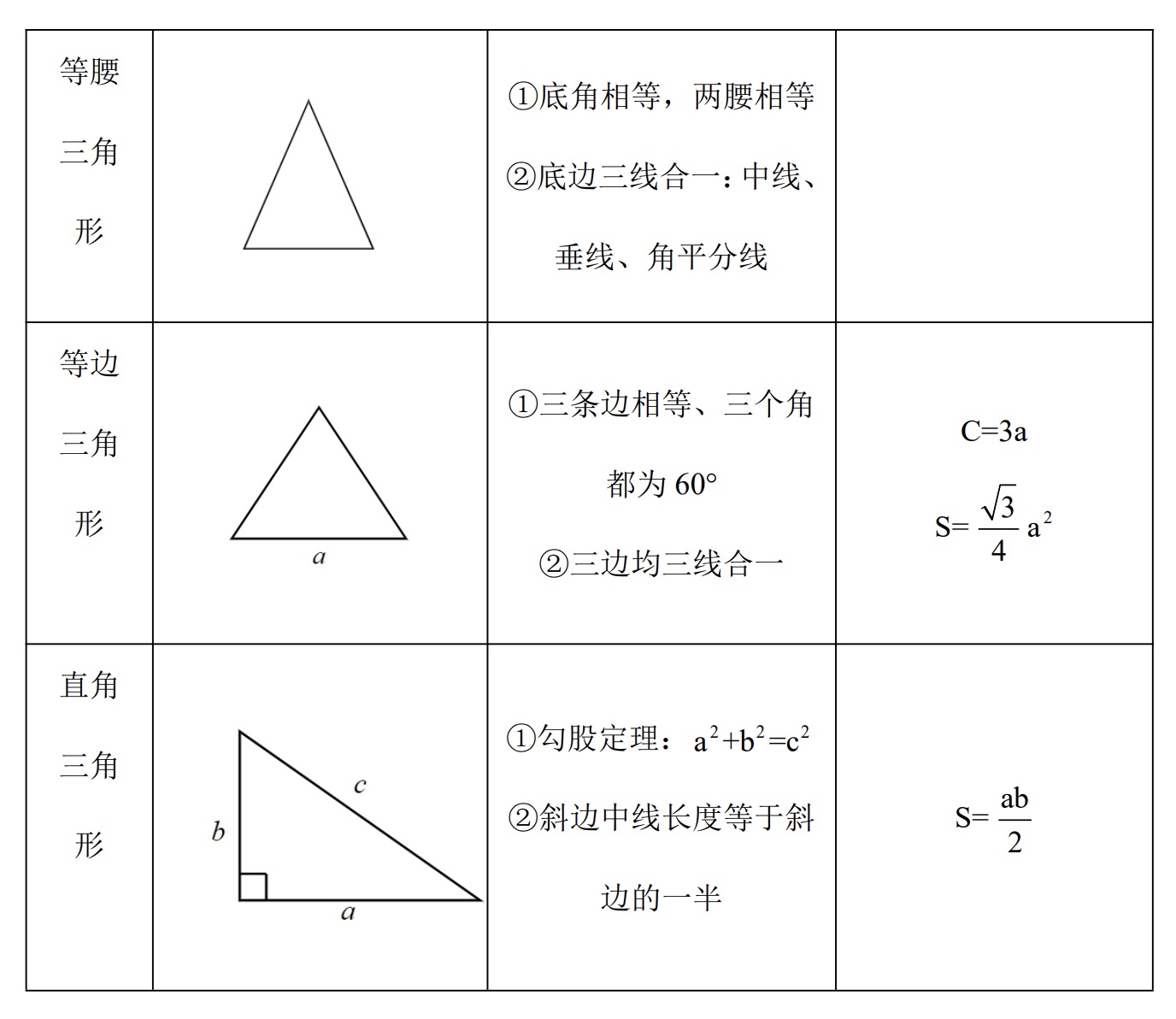
常见平面图形
补充
- 两个三角形,若对应高相等,则对应底边之比 = 面积之比。
常见勾股数(成比例即可)
3、4、5
6、8、10
5、12、13
7、24、25
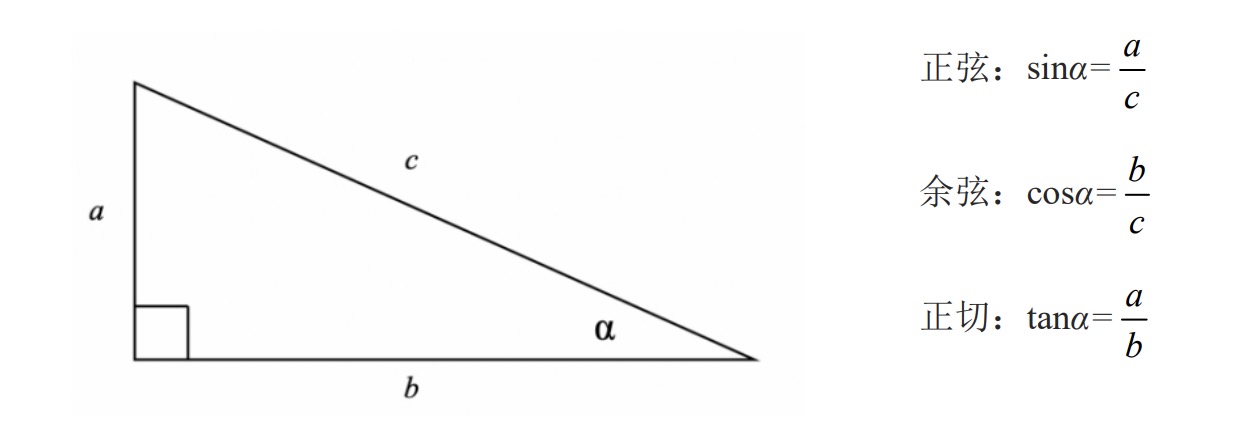
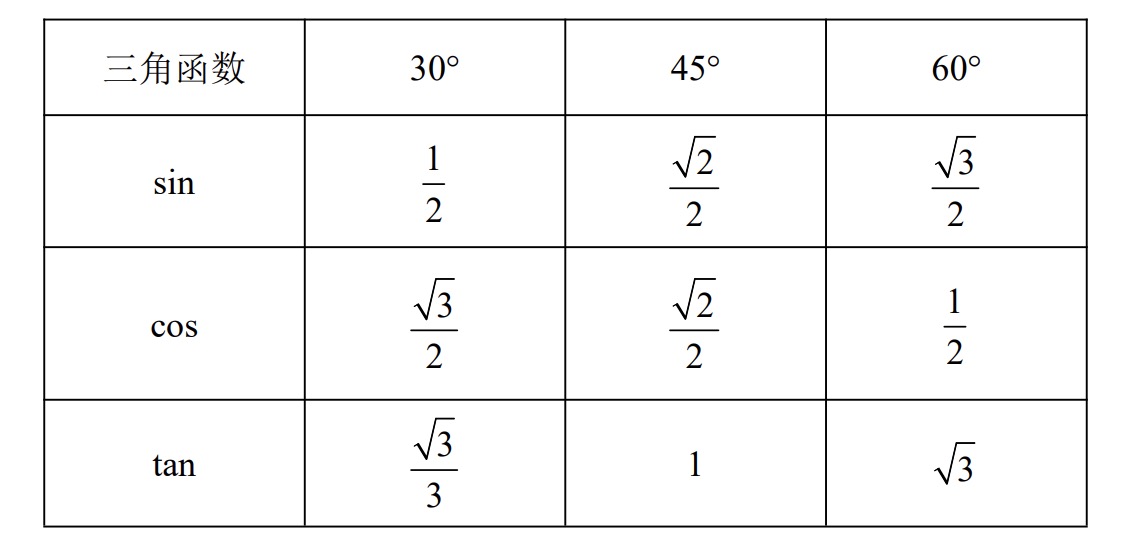
三角函数
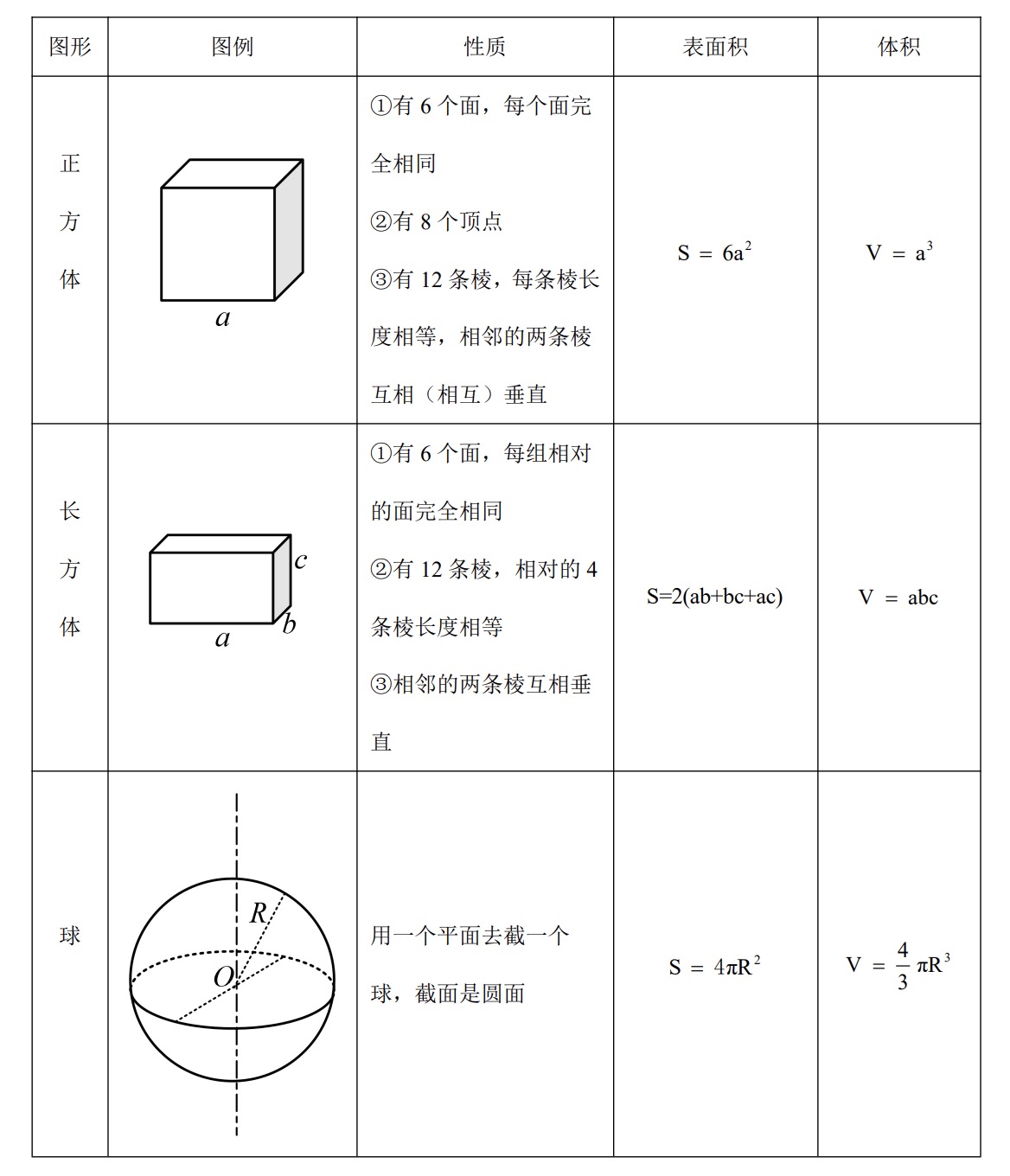
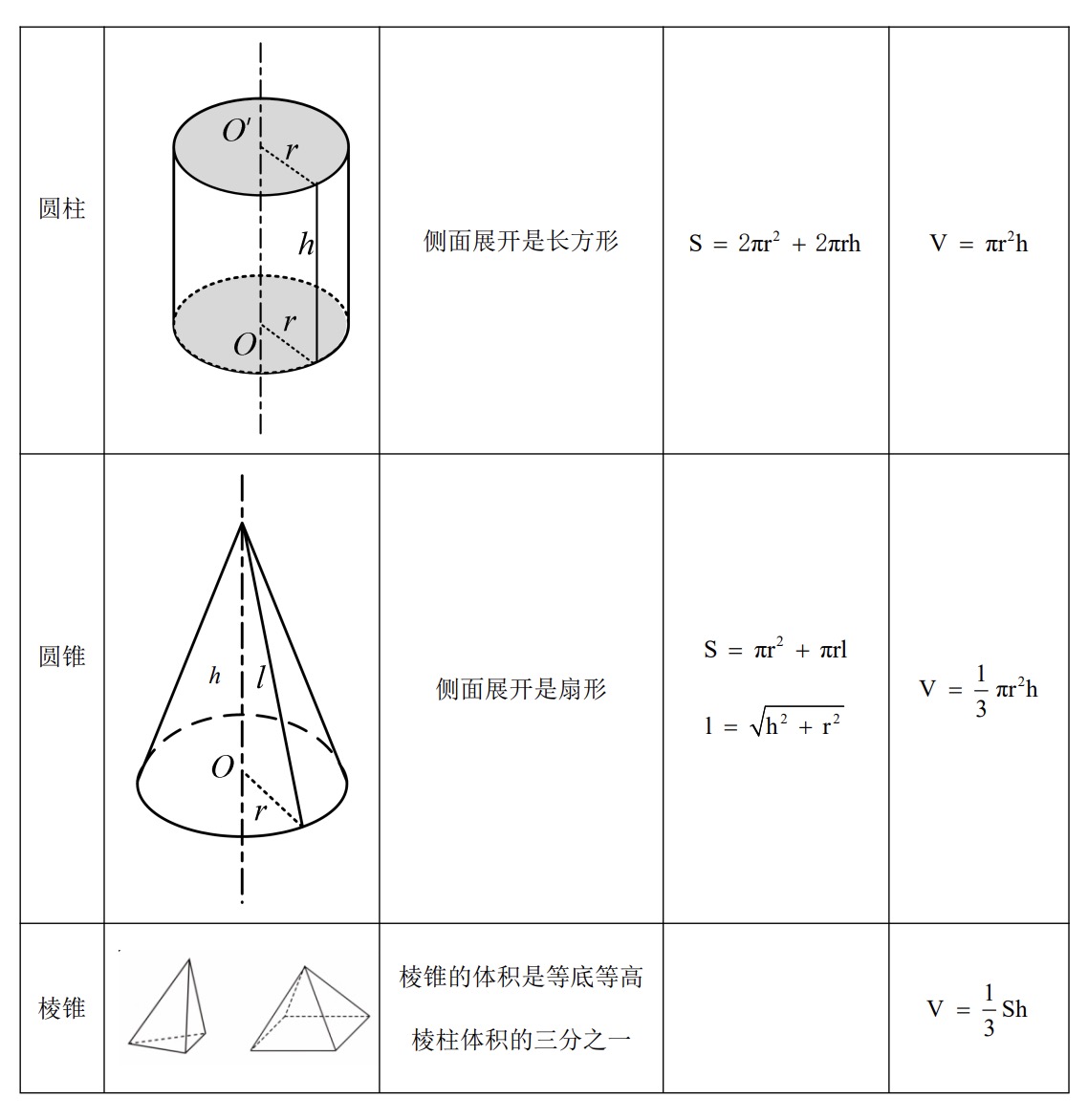
# 立体几何
# 几何特性
1. 最短路径问题
解题依据:
两点之间线段最短;
垂线段最短;
三角形两边之和大于第三边。
解题思路:
同一平面内:两个点在线段同侧,做一个点的对称点,对称点与另一个点的连线,即为最短路径长度。
立体图形:找到运动轨迹,展开立体图形后连接已知点(注意展开方式可以有多种)。
记住一个结论
展开后的图形,两个直角边的长度越接近,斜边越短。
2. 放缩特性
若将一个图形的边长变为原来的
对应角不变
周长变为原来的
倍 面积变为原来的
倍 体积变为原来的
倍
3. 相似三角形
判定条件:
两个角对应相等
三条边对应成比例
两边成比例且夹角相等
性质:
周长之比 = 对应边之比 = 相似比
面积之比 = 相似比的平方
# 排列组合
# 概念和计算方法
排列:从 m 个不同元素中,任取 n 个元素按照一定顺序排列。
组合:从 m 个不同元素中,任取 n 个元素组成一组。
# 分类与分步
分类用加法,分步用乘法
分类:一步完成,任选其一即可。
分步:多步完成,每一步都不能少。
# 枚举法
- 数据量较小时,可有序列出。
# 捆绑法
题型特征:出现 “相邻”、“在一起”、“挨着”
解题思路:
把相邻的元素捆绑起来,注意内部有无顺序;
将捆绑后的看成一个元素,再进行后续排列。
# 插空法
题型特征:出现 “不相邻”、“不相连”
解题思路:
先安排可以相邻的元素;
将不相邻的元素插入到空位中。
# 隔板法
题型特征:m 个相同的元素分给 n 个不同的主体(每人至少分一个)
解题思路:情况数 =
# 圆桌排列
- n 个不同元素围成一圈,共有
种排法。
# 平均分组
若平均分 n 组,不涉及顺序要求,最后要除以
剔重复。 例子
将 10 名运动员平均分成两组进行对抗赛,问有多少种不同的分法?答:
。 9 名运动员平均分 3 组进行对抗赛,有多少种不同分法?答:
。 13 个球队分 3 组,一组 5 个队,其它两组 4 个队,有多少种分法?答:
。 县公安局计划举办篮球比赛,6 支报名参赛的队伍将平均分为上午组和下午组进行小组赛。其中甲队与乙队来自同部门,不能分在同一组,则分组情况共有几种可能。
- 答:注意此题有涉及顺序,因此不用剔除重复。先排甲乙两队,有甲在上午、乙在下午,甲在下午、乙在上午 2 种可能,然后再对剩下的四支队伍进行分组,有
种可能,故总共有 种可能。
- 答:注意此题有涉及顺序,因此不用剔除重复。先排甲乙两队,有甲在上午、乙在下午,甲在下午、乙在上午 2 种可能,然后再对剩下的四支队伍进行分组,有
# 概率
# 给情况求概率
# 给概率求概率
1. 给概率求概率
分类用加法:分类概率 =
分步用乘法:分步概率 =
2. 正难反易
P(满足条件)= 1 - P(不满足条件)
# 杂项问题
# 容斥问题
1. 两集合容斥
- A + B + 都不 = 总数 + A ∩ B
2. 三集合容斥
A + B + C + 都不 = 总数 + A ∩ B + B ∩ C + A ∩ C - A ∩ B ∩ C
A + B + C + 都不 = 总数 + 只满足两条件 + 满足三条件 × 2
A + B + C + 都不 = 总数 + 满足两条件及以上 + 满足三条件
注意
在容斥问题中,“同时满足两个条件” 的语言表达就相当于 “只满足两个条件”。
# 溶液问题
1. 核心公式
浓度 = 溶质 / 溶液
溶液 = 溶质 + 溶剂
2. 反复操作类(溶液总质量不变)
题目特征:反复倒出部分溶液再用清水补满,求最终的浓度。
解题方法:最初浓度连续乘以剩余溶质占比。
3. 混合类溶液问题
题目特征:几种溶液混合形成新溶液。
解题方法:根据混合浓度 = 总溶质 / 总溶液,列方程求解。
# 年龄问题
核心思路:年龄差不变
公式:年龄 = 当年年份 - 出生年份
解题技巧:代入排除法,方程法,利用常识解题
注意
如果题干中同时出现爸爸和妈妈的年龄关系,并且要求其中一方的年龄,那么选项中一般会有两个选项分别是爸爸和妈妈的年龄,此时可以根据题干给出的关系配合这两个选项快速确定他们各自的年龄。
# 周期问题
非时间周期:总量 ÷ 周期,余几往后数几个元素
时间周期:经过的时间 ÷ 周期,余几往后数几个时间单位
下次相遇周期:求各个小周期的最小公倍数,算出大周期,往后查一个大周期的时间,即下次相遇的时间
注意
每隔 N 天 = 每过 N + 1 天;
涉及星期的问题周期为 7;
涉及年份等时间的周期,注意是闰年还是平年。
# 植树问题
1. 直线植树(两端植树)
段数 = S ÷ 间隔
棵数 = 段数 + 1
2. 安装吊灯(两端不装)
段数 = S ÷ 间隔
棵数 = 段数 - 1
3. 环形植树
段数 = S ÷ 间隔
棵数 = 段数
4. 爬楼梯
爬楼问题建议列表分析,不容易出错
爬到 n 层 = 爬了(n - 1)层
5. 最少植树问题
- 最少植树棵数 = 总距离 ÷ 各段距离的最大公约数 + 1
6. 不需要移动问题
不需要移动的树的间隔是原来和现在的间隔的最小公倍数,然后再利用直线植树的棵数计算方法算出不需要移动的树。
不需要移动棵数 = 段数的最大公约数 + 1(双边 = 单边 × 2)
# 猜题思维
# 排除干扰选项法
所求量与题干中其他量间有倍数、比例关系
题干中有部分和整体关系
# 目测法
# 常识秒杀法
# 倍数特性法
# 奇偶特性法
资料分析 →