常见数据结构在线演示网站：VisuAlgo.net/en (opens new window)。

列表

列表的定义

• 列表是一组有序的数据。每个列表中的数据项称为元素。元素的数量受内存控制。

• 不包含任何元素的列表称为空列表。

列表的使用场景

• 日常生活中，我们使用购物清单、待办事项列表都是列表。计算机中的列表也一样。

• 元素不是很多。

• 不需要很长序列查找元素或者排序。

• 列表是一种最自然的数据组织方式。

迭代器的优点

• 访问元素时不必关心底层数据结构。

• 增加和删除元素要比 for 更加灵活。

• 迭代器访问列表里的元素提供了统一的方法。

列表的代码实现

function List() {
  this.listSize = 0; // 列表元素个数
  this.pos = 0; // 列表当前位置
  this.dataStore = []; // 初始化一个空数组用来保存列表元素
  this.clear = clear; // 清空列表中的所有元素
  this.find = find; // 查找元素
  this.toString = toString; // 返回列表的字符串形式
  this.insert = insert; // 在现有元素后面插入新元素
  this.append = append; // 在列表元素末尾添加新元素
  this.remove = remove; // 从列表中删除元素
  this.front = front; // 从列表的当前位置移动到第一个位置
  this.end = end; // 从列表的当前位置移动到最后一个位置
  this.prev = prev; // 将当前位置前移一位
  this.next = next; // 将当前位置后移一位
  this.length = length; // 列表包含的元素个数
  this.currPos = currPos; // 返回列表的当前位置
  this.moveTo = moveTo; // 将当前位置的元素移动到指定位置
  this.getElement = getElement; // 获取当前的元素
  this.contains = contains; // 是否包含某个元素
}

// 在列表元素末尾添加新元素
function append(element) {
  this.dataStore[this.listSize++] = element;
}

// 查找元素
function find(element) {
  // 注意此处 ++ 应该置于 i 之前，以便返回正确的索引
  for (var i = 0; i < this.dataStore.length; ++i) {
    if (this.dataStore[i] === element) {
      return i;
    }
  }
  return -1;
}

// 从列表中删除元素
function remove(element) {
  var foundAt = this.find(element);
  if (foundAt > -1) {
    this.dataStore.slice(foundAt, 1);
    --this.listSize;
    return;
  }
  return false;
}

// 列表包含的元素个数
function length() {
  return this.listSize;
}

// 返回列表的字符串形式
function toString() {
  return this.dataStore;
}

// 在现有元素后面插入新元素
function insert(element, after) {
  var insertPos = this.find(after);
  if (insertPos > -1) {
    this.dataStore.splice(insertPos + 1, 0, element);
    ++this.listSize;
    return true;
  }
  return false;
}

// 清空列表中的所有元素
function clear() {
  delete this.dataStore;
  this.dataStore.length = 0; // 创建一个空数组
  this.listSize = this.pos = 0;
}

// 是否包含某个元素
function contains(element) {
  for (var i = 0; i < this.dataStore.length; i++) {
    if (this.dataStore[i] === element) {
      return true;
    }
  }
  return false;
}

// 从列表的当前位置移动到第一个位置
function front() {
  this.pos = 0;
}

// 从列表的当前位置移动到最后一个位置
function end() {
  this.pos = this.listSize - 1;
}

// 将当前位置前移一位
function prev() {
  if (this.pos > 0) {
    --this.pos;
  }
}

// 将当前位置后移一位
function next() {
  if (this.pos < this.listSize) {
    ++this.pos;
  }
}

// 返回列表的当前位置
function currPos() {
  return this.pos;
}

// 将当前位置的元素移动到指定位置
function moveTo(position) {
  this.pos = position;
}

// 获取当前的元素
function getElement() {
  return this.dataStore[this.pos];
}

列表的实际应用

var names = new List();
names.append("小白");
names.append("小王");
names.append("小红");
// names.next();
// console.log(names.getElement());

// 迭代器
for (names.front; names.currPos() < names.length(); names.next()) {
  console.log(names.getElement());
}

栈

栈的概念和用途

• 栈是一种特殊的列表。

• 栈是一种高效的数据结构，因为数据只能在栈顶删除或增加，操作很快。

• 栈的使用遍布程序语言实现的方方面面，从表达式求值到处理函数调用。

栈的一些关键点

• 栈内元素只能通过列表的一端访问，这一端称为栈顶（反之栈底）。

• 栈被称为一种后入先出（LIFO，last-in-first-out）的数据结构。

• 插入新元素又称作进栈、入栈或压栈，从一个栈删除元素又称作出栈或退栈。

栈的代码实现

function Stack() {
  this.dataStore = []; // 保存栈内元素
  this.top = 0; // 标记可以插入新元素的位置，栈内压入元素该变量变大，弹出元素该变量变小
  this.push = push; // 入栈操作
  this.pop = pop; // 出栈操作
  this.peek = peek; // 返回栈顶元素
  this.clear = clear; // 清空栈
  this.length = length; // 栈的长度
  this.isEmpty = isEmpty; // 判断栈是否为空
}

// 向栈中压入元素，同时让指针 top+1，一定注意++
function push(element) {
  this.dataStore[this.top++] = element;
  // this.dataStore.push(element);
}

// 出栈操作，同时将 top-1
function pop() {
  return this.dataStore[--this.top];
  // return this.dataStore.pop();
}

// 返回栈顶元素，top-1，返回不删除
function peek() {
  return this.dataStore[this.top - 1];
  // return this.dataStore[this.dataStore.length - 1];
}

// 返回栈内元素个数
function length() {
  return this.top;
  // return this.dataStore.length;
}

// 清空栈
function clear() {
  this.top = 0;
  // this.dataStore = [];
}

// 判断栈是否为空
function isEmpty() {
  return this.top === 0;
  // return this.dataStore.length === 0;
}

var stack = new Stack();
stack.push(1);
stack.push(2);
console.log("栈的长度：", stack.length());
console.log("栈顶元素：", stack.peek());
console.log("出栈元素：", stack.pop());
console.log("栈顶元素：", stack.peek());

用两个栈实现队列

题目地址 (opens new window)

入队始终操作 stack1，出队和获取头节点始终操作 stack2。

function StackQueue() {
  var stack1 = new Stack(); //负责添加元素
  var stack2 = new Stack(); //负责删除元素

  // 入队
  this.enqueue = function(item) {
    stack1.push(item);
  };

  // 队头元素
  this.head = function() {
    if (stack1.isEmpty() && stack2.isEmpty()) {
      return null;
    }
    while (stack2.isEmpty()) {
      while (!stack1.isEmpty()) {
        stack2.push(stack1.pop());
      }
    }
    return stack2.peek();
  };

  // 队列大小
  this.size = function() {
    if (!stack1.isEmpty()) {
      return stack1.length();
    } else {
      if (!stack2.isEmpty()) {
        return stack2.length();
      } else {
        return 0;
      }
    }
  };

  // 出队
  this.dequeue = function() {
    if (stack1.isEmpty() && stack2.isEmpty()) {
      return null;
    }
    while (stack2.isEmpty()) {
      while (!stack1.isEmpty()) {
        stack2.push(stack1.pop());
      }
    }
    return stack2.pop();
  };
}

var sQueue = new StackQueue();
sQueue.enqueue(1);
sQueue.enqueue(2);
sQueue.enqueue(3);
console.log(sQueue.head()); // 1
console.log(sQueue.dequeue()); // 1
console.log(sQueue.head()); // 2
console.log(sQueue.size()); // 2
console.log(sQueue.dequeue()); // 2
console.log(sQueue.dequeue()); // 3
console.log(sQueue.size()); // 0

验证回文串

题目地址 (opens new window)

var isPalindrome = function(s) {
  s = s.replace(/[^a-zA-Z0-9]/g, "").toLowerCase();
  const stack = [];
  for (let i = 0; i < s.length; i++) {
    stack.push(s[i]);
  }
  let reverse = "";
  while (stack.length) {
    reverse += stack.pop();
  }
  return reverse === s;
};

判断括号是否合法

题目地址 (opens new window)

var isValid = function(s) {
  if (s.length % 2 !== 0) return false;
  const stack = [];
  for (const c of s) {
    switch (c) {
      case "(":
      case "{":
      case "[":
        stack.push(c);
        break;
      case ")":
        if (stack.pop() !== "(") return false;
        break;
      case "}":
        if (stack.pop() !== "{") return false;
        break;
      case "]":
        if (stack.pop() !== "[") return false;
    }
  }
  return stack.length === 0;
};

var isValid = function(s) {
  if (s.length % 2 !== 0) return false;
  const stack = [];
  const bracket = {
    "(": ")",
    "{": "}",
    "[": "]"
  };
  for (const c of s) {
    if (c in bracket) {
      stack.push(c);
    } else if (stack.length === 0 || bracket[stack.pop()] !== c) {
      return false;
    }
  }
  return stack.length === 0;
};

// 只能用于判断一种括号
function is_legal_brackets(s) {
  const stack = new Stack();
  for (var i = 0; i < s.length; i++) {
    //遇到左括号，入栈
    if (s[i] == "(") {
      stack.push(s[i]);
    } else if (s[i] == ")") {
      //遇到右括号，先判断栈是否为空
      if (stack.isEmpty()) {
        return false;
      } else {
        stack.pop(); //弹出左括号
      }
    }
  }
  //如果栈为空，说明该字符串括号合法
  return stack.isEmpty();
}

最长有效括号

题目地址 (opens new window)

var longestValidParentheses = function(s) {
  let res = 0;
  const stack = [-1];
  for (let i = 0; i < s.length; i++) {
    if (s[i] === "(") {
      stack.push(i); // 左括号的索引入栈
      continue; // 跳过，考察下一个符号
    }
    stack.pop(); // 遇到右括号，栈顶出栈
    if (!stack.length) {
      stack.push(i); // 如果栈顶因此为空，说明该更换栈顶索引了
    } else {
      res = Math.max(res, i - stack[stack.length - 1]); // 比较获取最大的有效长度
    }
  }
  return res;
};

计算后缀表达式（逆波兰表达式）

function calc_exp(exp) {
  var stack = new Stack();
  for (var i = 0; i < exp.length; i++) {
    var item = exp[i];
    if (["+", "-", "*", "/"].indexOf(item) >= 0) {
      // 从栈顶弹出两个元素
      var value1 = stack.pop();
      var value2 = stack.pop();
      // 拼成表达式
      var exp_str = value2 + item + value1; // 第一次弹出的数放在运算符右边，第二次弹出的数放在运算符左边
      // 计算并取整
      var res = parseInt(eval(exp_str)); // eval() 函数可计算某个字符串，并执行其中的的 JavaScript 代码
      // 将计算结果压入栈
      stack.push(res.toString());
    } else {
      stack.push(item);
    }
  }
  // 若表达式正确，最终栈里应只有一个元素，这就是表达式的值
  return stack.pop();
}
var exp1 = ["4", "13", "5", "/", "+"]; // (4 + (13 / 5)) = 6
// var exp2 = ['10','6','9','3','+','-11','*','/','*','17','+','5','+'];  // ((10 * (6 / ((9 + 3) * -11))) + 17) + 5 = 22
console.log(calc_exp(exp1));
console.log(calc_exp(exp2));

十进制转二进制

function BinaryConversion(number) {
  var stack = new Stack();
  var remainder;
  var binary = ""; // 存储二进制
  while (number > 0) {
    remainder = number % 2; // 求模取余
    stack.push(remainder);
    number = Math.floor(number / 2); // 向下取整
  }
  while (!stack.isEmpty()) {
    binary += stack.pop();
  }
  return binary;
}
console.log(BinaryConversion(10)); // 1010

队列

队列的概念和用途

• 队列是一种特殊的列表。

• 队列可以想像成银行前排队的人群，排在最前面的人第一个办理业务，新来的人在后面排队，直到轮到他为止。

• 队列被用在很多地方，比如打印任务池，提交操作系统执行的一系列流程。

队列的一些关键点

• 队列只能在队尾插入元素，在队首删除元素。

• 队列是一种先进先出（FIFO，First-In-First-Out）的数据结构。

• 插入新元素称作入队，删除元素称作出队。

注意

有一些特殊情况，在删除元素时不必遵守先进先出的约定，比如急诊。这种场景我们需要使用优先队列这种数据结构来模拟。

队列的代码实现

function Queue() {
  this.dataStore = [];
  this.enqueue = enqueue; // 入队
  this.dequeue = dequeue; // 出队
  this.head = head; // 获取队首元素
  this.tail = tail; // 获取队尾元素
  this.length = length; // 获取队列长度
  this.isEmpty = isEmpty; // 判断队列是否为空
  this.clear = clear; // 清空队列
  this.toString = toString; // 显示队列中的所有元素
}

// 入队
function enqueue(element) {
  this.dataStore.push(element);
}

// 出队
function dequeue() {
  return this.dataStore.shift();
}

// 获取队首元素
function head() {
  return this.dataStore[0];
}

// 获取队尾元素
function tail() {
  return this.dataStore[this.dataStore.length - 1];
}

// 获取队列长度
function length() {
  return this.dataStore.length;
}

// 判断队列是否为空
function isEmpty() {
  return this.dataStore.length === 0;
}

// 清空队列
function clear() {
  this.dataStore = [];
}

// 显示队列中的所有元素
function toString() {
  var str = "";
  for (var i = 0; i < this.dataStore.length; i++) {
    str += this.dataStore[i] + "\n";
  }
  return str;
}

var queue = new Queue();
queue.enqueue(1);
queue.enqueue(2);
console.log(queue.toString()); // 1 2
queue.dequeue();
console.log(queue.toString()); // 2

用两个队列实现栈

题目地址 (opens new window)

function QueueStack() {
  var queue1 = new Queue();
  var queue2 = new Queue();
  var data_queue = new Queue(); // 存放数据的队列
  var empty_queue = new Queue(); // 空队列

  // 初始化队列，用来改变 data_queue 和 empty_queue 的指向
  // 让 data_queue 始终指向有数据的队列，empty_queue 始终指向空队列
  var init_queue = function() {
    if (queue1.isEmpty() && queue2.isEmpty()) {
      data_queue = queue1;
      empty_queue = queue2;
    } else if (queue1.isEmpty()) {
      data_queue = queue2;
      empty_queue = queue1;
    } else {
      data_queue = queue1;
      empty_queue = queue2;
    }
  };

  // 入栈
  this.push = function(item) {
    init_queue();
    data_queue.enqueue(item);
  };

  // 栈顶元素
  this.top = function() {
    init_queue();
    return data_queue.tail();
  };

  // 出栈
  this.pop = function() {
    init_queue();
    while (data_queue.length() > 1) {
      empty_queue.enqueue(data_queue.dequeue());
    }
    return data_queue.dequeue();
  };

  // 栈是否为空
  this.empty = function() {
    return data_queue.isEmpty();
  };
}
var qStack = new QueueStack();
qStack.push(1);
console.log(qStack.top()); // 1
qStack.push(2);
console.log(qStack.top()); // 2
qStack.push(3);
console.log(qStack.top()); // 3
console.log(qStack.pop()); // 3
console.log(qStack.pop()); // 2
console.log(qStack.top()); // 1
console.log(qStack.empty()); // false
console.log(qStack.pop()); // 1
console.log(qStack.empty()); // true

最近的请求次数

题目地址 (opens new window)

var RecentCounter = function() {
  this.queue = [];
};
RecentCounter.prototype.ping = function(t) {
  this.queue.push(t);
  while (this.queue[0] < t - 3000) {
    this.queue.shift();
  }
  return this.queue.length;
};

约瑟夫环

function del_ring(arr_list) {
  var queue = new Queue();
  // 将数组里的元素放入队列
  for (var i = 0; i < arr_list.length; i++) {
    queue.enqueue(arr_list[i]);
  }
  var index = 0;
  while (queue.length() !== 1) {
    // 弹出一个元素，判断是否需要删除
    var item = queue.dequeue();
    index += 1;
    // 每隔两个就要删除掉⼀一个，那么不不是被删除的元素就放回到队列列尾部
    if (index % 3 !== 0) {
      queue.enqueue(item);
    }
  }
  return queue.head();
}
var arr_list = [];
for (var i = 0; i < 100; i++) {
  arr_list.push(i);
}
console.log(del_ring(arr_list));

斐波那契数列

function fibonacci(n) {
  queue = new Queue();
  var index = 0;
  // 先放入斐波那契序列的前两个数
  queue.enqueue(1);
  queue.enqueue(1);
  while (index < n - 2) {
    // 出一个队列元素
    var del_item = queue.dequeue();
    // 取队列头部元素
    var head_item = queue.head();
    var next_item = del_item + head_item;
    // 将计算结果放入队列
    queue.enqueue(next_item);
    index += 1;
  }
  return queue.tail();
}
console.log(fibonacci(8)); // 21

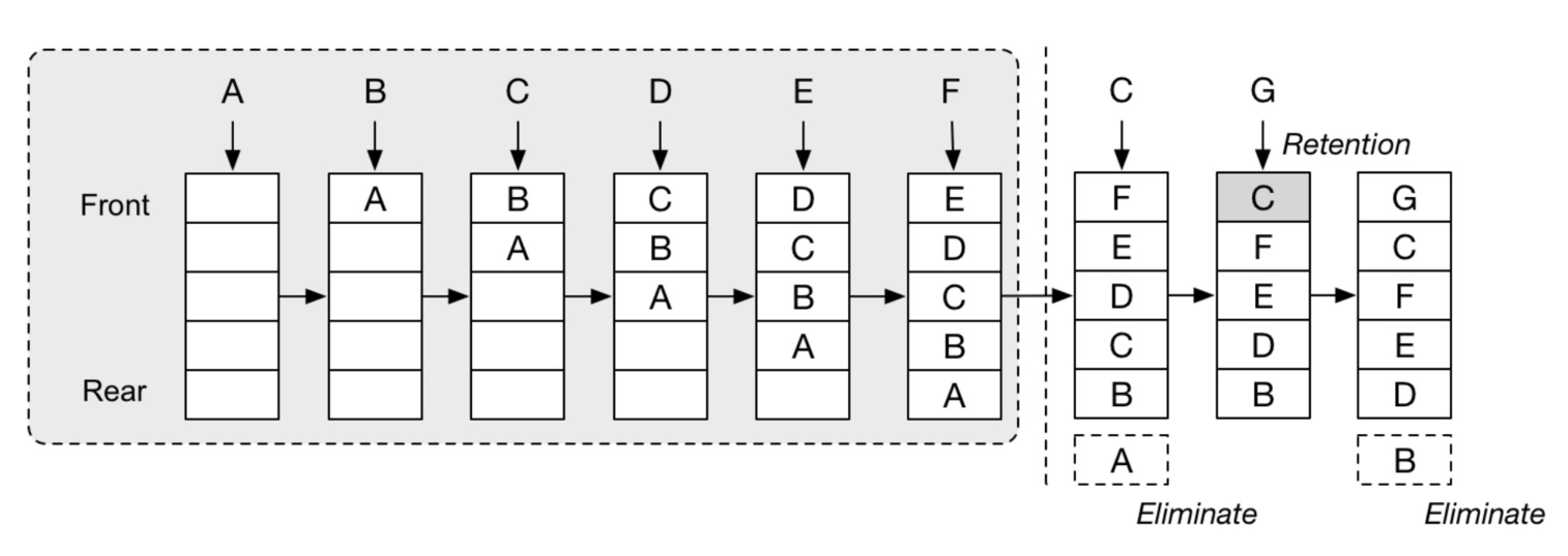
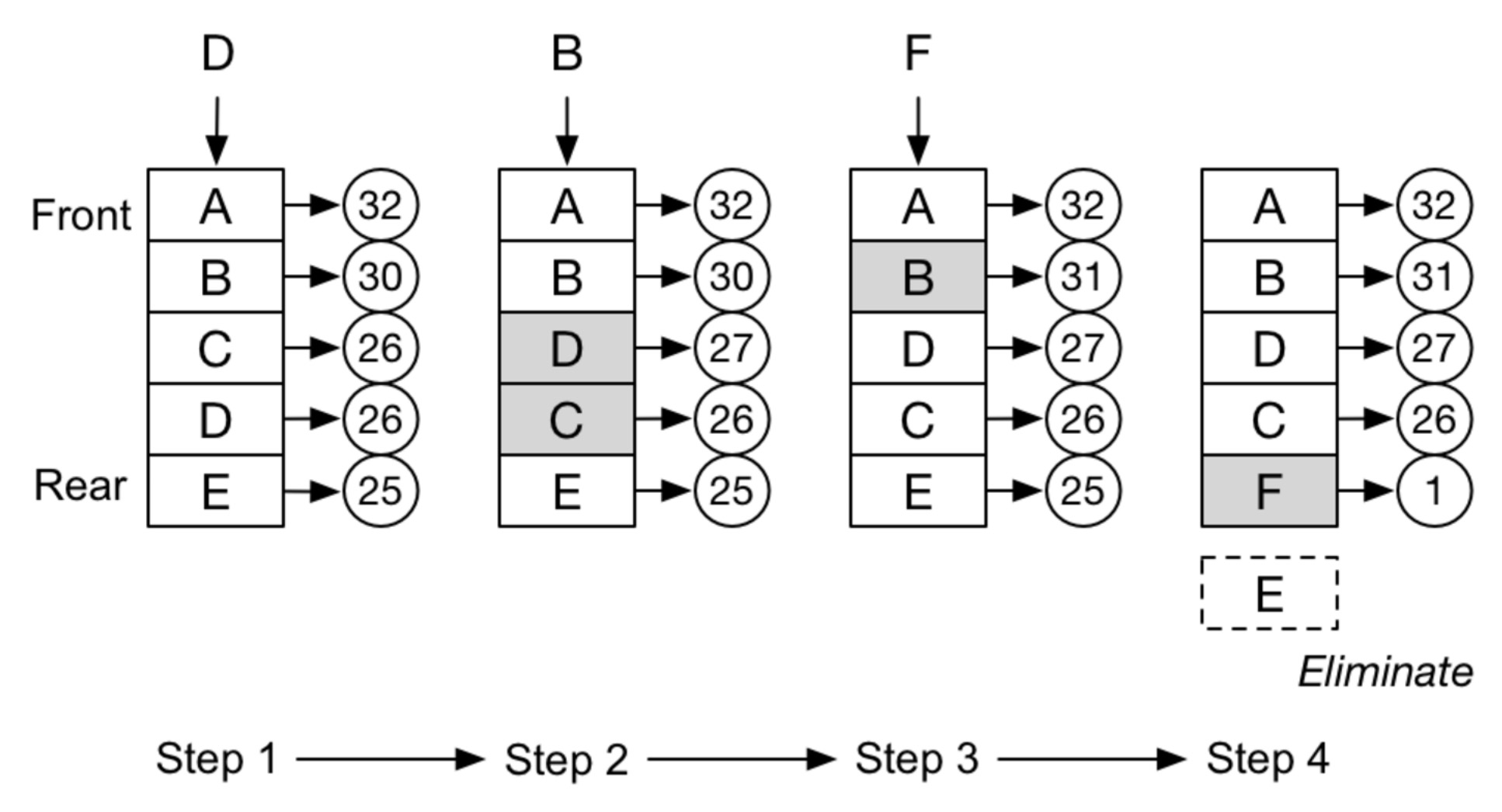
循环队列，实现击鼓传花

function drumming(names, number) {
  var queue = new Queue();
  for (var i = 0; i < names.length; i++) {
    queue.enqueue(names[i]);
  }
  while (queue.length() > 1) {
    for (var i = 0; i < number - 1; i++) {
      queue.enqueue(queue.dequeue());
    }
    var dieout = queue.dequeue();
    console.log("此轮被淘汰的玩家是：" + dieout);
  }
  console.log("游戏的最终赢家是：" + queue.dequeue());
}
// 玩家列表
var names = ["a", "b", "c", "d", "e", "f"];
// 游戏规则：从一名玩家开始传花，当传到第3次的时候，花在谁手里，谁就被淘汰，直到最后只剩一名玩家。
var number = 3;
drumming(names, number);

实现优先队列

// 优先队列：出队的时候跟普通队列一样，主要是入队的时候比较麻烦，要考虑到优先级的问题
function PriorityQueue() {
  var items = [];

  // 辅助类
  var QueueItem = function(item, priority) {
    this.item = item; // 元素
    this.priority = priority; // 优先级
  };

  // 入队
  this.enqueue = function(item, priority) {
    var queueItem = new QueueItem(item, priority);
    var isAdd = false; // 判断是否插入成功
    for (var i = 0; i < items.length; i++) {
      if (queueItem.priority > items[i].priority) {
        // 遍历元素比较优先级
        items.splice(i, 0, queueItem); // 重点！从索引为 i 的位置开始切，切 0 个，并替换成 queueItem。巧妙地使用 splice 这个函数实现了元素的插入
        isAdd = true;
        break;
      }
    }
    if (!isAdd) {
      // 貌似有点懂了
      items.push(queueItem);
    }
  };

  this.getItems = function() {
    return items;
  };
}
var pq = new PriorityQueue();
pq.enqueue("小红", 12);
pq.enqueue("小明", 10);
pq.enqueue("小黑", 11);
console.log(pq.getItems());

链表

链表的概念和用途

• 数组不是组织数据的最佳结构。

• JavaScript 的数组被实现成了对象，与其他语言的数组相比，效率低了很多。

• 如果你发现数组实际使用很慢，就可以考虑用链表替代它。除了对数据的随机访问，链表几乎可以用在任何可以使用一维数组的地方。

链表的一些关键点

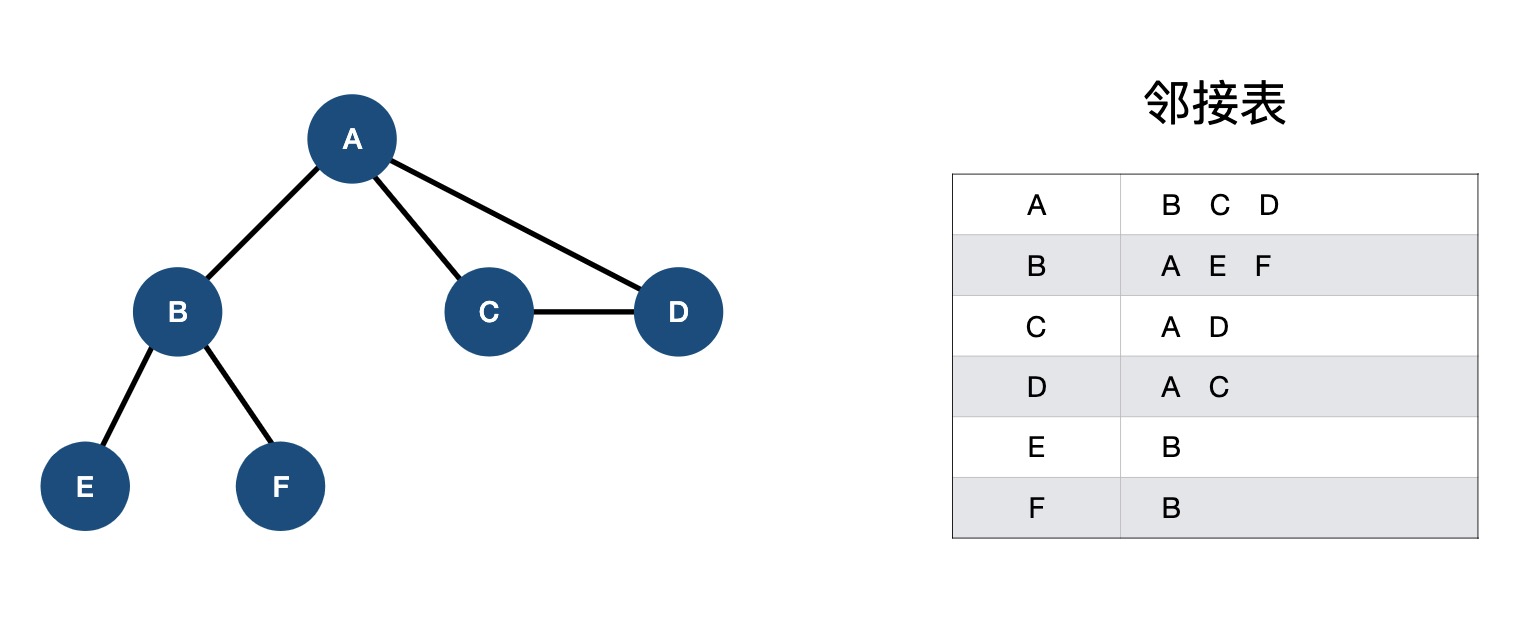
• 链表是由一系列节点组成的集合，每个节点都使用一个对象的引用指向它的后继，指向另一个节点的引用叫做链。

• 链表元素靠相互之间关系进行引用 A -> B -> C，B 并不是链表的第二个元素而是 B 跟在 A 后面。遍历链表就是跟着链表，从链表的首节点一直到尾节点，但不包含头节点，头节点常常被称为链表的接入点。（链表的尾节点指向一个 null 节点）

• 向单向链表插入一个节点，需要修改它前面的节点（前驱）使其指向新加入的节点，而新加入的节点则指向原来前驱节点指向的节点。

• 从单向链表删除一个节点，需要将待删除节点的前驱节点指向待删除节点的后继节点，同时删除的节点指向 null 节点。

单向链表的代码实现

// 节点类
function Node(data) {
  this.data = data;
  this.next = null;
}

// 链表类
function LinkList() {
  this.head = new Node("head");
  this.find = find;
  this.insert = insert;
  this.findPrev = findPrev;
  this.remove = remove;
  this.display = display;
}

// 找到当前节点
function find(data) {
  var currentNode = this.head;
  while (currentNode.data !== data) {
    currentNode = currentNode.next;
  }
  return currentNode;
}

// 在当前节点之后插入新节点
function insert(newData, data) {
  var newNode = new Node(newData);
  var currentNode = this.find(data);
  newNode.next = currentNode.next;
  currentNode.next = newNode;
}

// 找到当前节点的前驱节点
function findPrev(data) {
  var currentNode = this.head;
  while (currentNode.next && currentNode.next.data !== data) {
    currentNode = currentNode.next;
  }
  return currentNode;
}

// 删除某个节点
function remove(data) {
  var prevNode = this.findPrev(data);
  var currentNode = this.find(data);
  if (prevNode.next) {
    prevNode.next = currentNode.next;
    currentNode.next = null; // 释放内存，防止内存泄漏
  }
}

// 打印整个链表
function display() {
  var currentNode = this.head;
  var linkArr = [];
  while (currentNode.next) {
    // 打印链表时不需要打印头节点
    linkArr.push(currentNode.next.data);
    currentNode = currentNode.next;
  }
  console.log(linkArr.join(" -> "));
}

var link = new LinkList();
link.insert("first", "head");
link.insert("second", "first");
link.insert("third", "second");
link.display(); // first -> second -> third
link.remove("second");
link.display(); // first -> third

双向链表的代码实现

// 节点类
function Node(data) {
  this.data = data;
  this.prev = null;
  this.next = null;
}

// 链表类
function LinkList() {
  this.head = new Node("head");
  this.find = find;
  this.insert = insert;
  this.remove = remove;
  this.display = display;
  this.findLast = findLast;
  this.displayReverse = displayReverse;
}

function find(data) {
  var currentNode = this.head;
  while (currentNode.data !== data) {
    currentNode = currentNode.next;
  }
  return currentNode;
}

// 在当前节点之后插入新节点，分尾节点和非尾节点两种情况
function insert(newData, data) {
  var newNode = new Node(newData);
  var currentNode = this.find(data);
  // 如果新节点插入的位置是尾节点
  newNode.next = currentNode.next;
  newNode.prev = currentNode;
  currentNode.next = newNode;
  // 如果新节点插入的位置不是尾节点
  if (newNode.next) {
    newNode.next.prev = newNode;
  }
}

// 删除某个节点，也分尾节点和非尾节点两种情况
function remove(data) {
  var currentNode = this.find(data);
  if (currentNode.next) {
    // 如果删除的节点不是尾节点
    currentNode.prev.next = currentNode.next;
    currentNode.next.prev = currentNode.prev;
    // 释放内存，防止内存泄漏
    currentNode.prev = null;
    currentNode.next = null;
  } else {
    // 如果删除的节点是尾节点
    currentNode.prev.next = null;
    currentNode.prev = null; // 释放内存，防止内存泄漏
  }
}

// 打印整个链表
function display() {
  var currentNode = this.head;
  var linkArr = [];
  while (currentNode.next) {
    // 打印链表时不需要打印头节点
    linkArr.push(currentNode.next.data);
    currentNode = currentNode.next;
  }
  console.log(linkArr.join(" < == > "));
}

// 找到最后一个节点
function findLast() {
  var currentNode = this.head;
  while (currentNode.next) {
    currentNode = currentNode.next;
  }
  return currentNode;
}

// 反向打印整个链表
function displayReverse() {
  var currentNode = this.findLast();
  var linkArr = [];
  while (currentNode.prev) {
    linkArr.push(currentNode.data);
    currentNode = currentNode.prev;
  }
  console.log(linkArr.join(" < == > "));
}

var link = new LinkList();
link.insert("first", "head");
link.insert("second", "first");
link.insert("third", "second");
link.display(); // first < == > second < == > third
link.remove("second");
link.display(); // first < == > third
link.displayReverse(); // third < == > first

链表的另外两种实现

// 定义链表类
function LinkList() {
  // 定义节点
  var Node = function(data) {
    this.data = data;
    this.next = null;
  };
  var length = 0; // 长度
  var head = null; // 头节点
  var tail = null; // 尾节点

  // 链表尾部添加一个节点
  this.append = function(data) {
    // 创建新节点
    var new_node = new Node(data);
    if (head === null) {
      head = new_node;
      tail = new_node;
    } else {
      tail.next = new_node;
      tail = new_node;
    }
    length++;
    return true;

    // 另一种实现方式
    // var node = new Node(data);
    // if (head == null) {
    //   head = node;
    // } else {
    //   var current = head;
    //   while (current.next) {
    //     current = current.next;
    //   }
    //   // while 循环执行完之后 ，current 已经是链表最后一项了
    //   current.next = node;
    // }
    // length++;
  };

  //打印链表
  this.print = function() {
    var curr_node = head;
    var linkArr = [];
    while (curr_node) {
      // console.log(curr_node.data);
      linkArr.push(curr_node.data);
      curr_node = curr_node.next; //遍历链表的核心
    }
    console.log(linkArr.join(" -> "));
  };

  //任意位置插入节点
  this.insert = function(index, data) {
    if (index < 0 || index > length) {
      // index 不合法
      return false;
    } else if (index === length) {
      // index === length,说明是在尾节点的后面新增,直接调用 append 方法即可
      return this.append(data);
    } else {
      var new_node = new Node(data);
      if (index === 0) {
        // 如果在头节点前面插入,新的节点就变成了了头节点
        new_node.next = head;
        head = new_node;
      } else {
        // 要插入的位置是 index，找到索引为 index-1 的节点，然后进行连接
        // var insert_index = 1;
        // var curr_node = head;
        // while(insert_index < index){
        //     insert_index++;
        //     curr_node = curr_node.next;
        // }
        // // index = 1，curr_node 指向 head，是第一个节点，
        // var next_node = curr_node.next;   // next_node 是第二个节点
        // curr_node.next = new_node;        // 第一个节点指向要插入的节点
        // new_node.next = next_node;        // 要插入的节点指向第二个节点

        // 另一种实现方式
        var pre_node = get_node(index - 1);
        new_node.next = pre_node.next;
        pre_node.next = new_node;
      }
      length++;
      return true;
    }
  };

  // 删除指定位置的节点
  this.removeAt = function(index) {
    if (index < 0 || index >= length) {
      // index 不合法
      return null;
    } else {
      var del_node = null; // 存放被删除的节点
      if (index === 0) {
        del_node = head;
        head = head.next;
      } else {
        var del_index = 0;
        var pre_node = null; // 被删除节点的前一个节点
        var curr_node = head; // 被删除的节点
        while (del_index < index) {
          del_index++;
          pre_node = curr_node;
          curr_node = curr_node.index;
        }
        del_node = curr_node;
        // 被删除节点的前一个节点指向被删除节点的后一个节点
        pre_node.next = curr_node.next;
        // 如果被删除的节点是尾节点
        if (curr_node.next === null) {
          tail = pre_node;
        }
      }
      length--;
      del_node.next = null;
      return del_node.data;
    }
  };

  /*
    // 另一种实现方式
    // 删除指定位置的节点
    this.removeAt = function(index) {
      // 参数不不合法
      if (index < 0 || index >= length) {
        return null;
      } else {
        var del_node = null;
        // 删除的是头节点
        if (index == 0) {
          // head 指向下一个节点
          del_node = head;
          head = head.next;
          // 如果 head == null，说明之前链表只有一个节点
          if(!head){
            tail = null;
          }
        } else {
          // 找到索引为 index-1 的节点
          var pre_node = get_node(index-1);
          del_node = pre_node.next;
          pre_node.next = pre_node.next.next;
          // 如果删除的是尾节点
          if(del_node.next==null){
            tail = pre_node;
          }
        }
        length -= 1;
        del_node.next = null;
        return del_node.data;
      }
    };
  */

  // removeAt(index)   删除某个位置的元素
  // indexOf(data)     获取某个元素的位置
  this.remove = function(data) {
    // length --
    return this.removeAt(this.indexOf(data));
  };

  // 获得指定位置的节点
  var get_node = function(index) {
    if (index < 0 || index >= length) {
      return null;
    }
    var curr_node = head;
    var node_index = index;
    while (node_index-- > 0) {
      curr_node = curr_node.next;
    }
    return curr_node;
  };
  // 返回指定位置节点的值
  this.get = function(index) {
    var node = get_node(index);
    if (node) {
      return node.data;
    }
    return null;
  };

  // 返回指定元素的索引，如果没有，返回-1；如果有多个相同元素，返回第一个
  this.indexOf = function(data) {
    var index = -1;
    var curr_node = head;
    while (curr_node) {
      index++;
      if (curr_node.data === data) {
        return index;
      } else {
        curr_node = curr_node.next;
      }
    }
    return -1;
  };

  // 返回链表的大小
  this.length = function() {
    return length;
  };

  // 删除尾节点
  this.remove_tail = function() {
    return this.remove(length - 1);
  };

  // 删除头节点
  this.remove_head = function() {
    return this.remove(0);
  };

  // 返回链表头节点的值
  this.head = function() {
    return this.get(0);
  };

  // 返回链表尾节点的值
  this.tail = function() {
    return this.get(length - 1);
  };

  // 判断链表是否为空
  this.isEmpty = function() {
    return this.length === 0;
  };

  // 清空链表
  this.clear = function() {
    head = null;
    tail = null;
    length = 0;
  };
}

var link = new LinkList();
link.append(1);
link.append(4);
link.append(9);
link.print();
console.log(link.head());

var LikedList = function() {
  // 链表头
  var head = null;
  // 链表长度
  var length = 0;

  // 辅助类：节点
  var Node = function(element) {
    this.element = element;
    this.next = null;
  };

  // 链表尾添加元素
  this.append = function(element) {
    var node = new Node(element);

    if (head == null) {
      head = node;
    } else {
      var current = head;
      while (current.next) {
        current = current.next;
      }
      // while 循环执行完之后 ，current 已经是链表最后一项了
      current.next = node;
    }
    length++;
  };

  // 链表某一个位置添加元素
  this.insert = function(position, element) {
    // 没有越界时
    if (position > -1 && position < length) {
      var node = new Node(element);
      if (position === 0) {
        var current = head;
        head = node;
        head.next = current;
      } else {
        var index = 0;
        var current = head;
        var previous = null;
        while (index < position) {
          previous = current;
          current = current.next;
          index++;
        }

        previous.next = node;
        node.next = current;
      }
      length++;
    }
  };

  this.removeAt = function(position) {
    if (position > -1 && position < length) {
      if (position === 0) {
        var current = head;
        head = current.next;
      } else {
        var current = head;
        var previous = null;
        var index = 0;
        while (index < position) {
          previous = current;
          current = current.next;
          index++;
        }
        // 跳出循环的时候 index === position
        previous.next = current.next;
      }

      length--;
      return current;
    }
    return null;
  };

  this.indexOf = function(element) {
    var current = head;
    var index = 0;
    while (current) {
      if (current.element === element) {
        return index;
      }
      current = current.next;
      index++;
    }
    return -1;
  };

  // removeAt(position)   删除某个位置的元素
  // indexOf(element)     获取某个元素的位置
  this.remove = function(element) {
    // length --
    return this.removeAt(this.indexOf(element));
  };

  this.isEmpty = function() {
    return length === 0;
  };
  this.size = function() {
    return length;
  };

  this.getHead = function() {
    return head;
  };
};

var l = new LikedList();
l.append(1);
l.append(2);
l.append(3);
l.insert(1, 10);
console.log(l.size());

反转链表

题目地址 (opens new window)

// 迭代解法
var reverseList = function(head) {
  if (!head || !head.next) {
    return head;
  }
  let prev = null;
  let cur = head;
  while (cur) {
    let next = cur.next;
    cur.next = prev;
    prev = cur;
    cur = next;
  }
  return prev;
};

// 递归解法
var reverseList = function(head) {
  if (!head || !head.next) {
    return head;
  }
  const newHead = reverseList(head.next);
  head.next.next = head;
  head.next = null;
  return newHead;
};

反转链表 II

题目地址 (opens new window)

var reverseBetween = function(head, left, right) {
  // 因为头节点有可能发生变化，使用虚拟头节点可以避免复杂的分类讨论
  const dummy = new ListNode();
  dummy.next = head;

  // 第 1 步：从虚拟头节点走 left - 1 步，来到 left 节点的前一个节点
  let prevLeftNode = dummy;
  for (let i = 0; i < left - 1; i++) {
    prevLeftNode = prevLeftNode.next;
  }

  // 第 2 步：从 pre 再走 right - left + 1 步，来到 right 节点
  let rightNode = prevLeftNode;
  for (let i = 0; i < right - left + 1; i++) {
    rightNode = rightNode.next;
  }

  // 第 3 步：切断出一个子链表（截取链表）
  let leftNode = prevLeftNode.next;
  let nextRightNode = rightNode.next;

  // 注意：切断链接
  prevLeftNode.next = null;
  rightNode.next = null;

  // 第 4 步：反转子链表
  reverseLinkedList(leftNode);

  // 第 5 步：接回到原来的链表中
  leftNode.next = nextRightNode;
  prevLeftNode.next = rightNode;

  return dummy.next;
};

function reverseLinkedList(head) {
  let prev = null,
    cur = head;
  while (cur) {
    let next = cur.next;
    cur.next = prev;
    prev = cur;
    cur = next;
  }
}

两两交换链表中的节点

题目地址 (opens new window)

var swapPairs = function(head) {
  const dummy = new ListNode(null); // 虚拟节点，用于返回最终的结果
  dummy.next = head;
  let prev = dummy; // 虚拟节点，用于协助交换
  while (head && head.next) {
    let first = head,
      second = head.next; // 实际要相互交换位置的两个节点
    prev.next = second;
    first.next = second.next;
    second.next = first;
    prev = first;
    head = first.next;
  }
  return dummy.next;
};

环形链表

题目地址 (opens new window)

var hasCycle = function(head) {
  if (!head || !head.next) {
    return false;
  }
  let slow = head;
  let fast = head.next;
  while (slow !== fast) {
    if (!fast || !fast.next) {
      return false;
    }
    slow = slow.next;
    fast = fast.next.next;
  }
  return true;
};

删除链表的节点

题目地址 (opens new window)

// 递归解法
var deleteNode = function(head, val) {
  if (head.val === val) {
    return head.next;
  }
  head.next = deleteNode(head.next, val);
  return head;
};

// 迭代解法
var deleteNode = function(head, val) {
  if (head.val === val) {
    return head.next;
  }
  let cur = head;
  while (cur.next) {
    if (cur.next.val === val) {
      cur.next = cur.next.next;
      break;
    }
    cur = cur.next;
  }
  return head;
};

// 双指针解法
var deleteNode = function(head, val) {
  if (head.val === val) {
    return head.next;
  }
  let prev = new ListNode(-1);
  let cur = head;
  prev.next = cur;
  while (cur) {
    if (cur.val === val) {
      prev.next = cur.next;
      break;
    }
    prev = prev.next;
    cur = cur.next;
  }
  return head;
};

删除链表中的节点

题目地址 (opens new window)

var deleteNode = function(node) {
  node.val = node.next.val;
  node.next = node.next.next;
};

两数相加

题目地址 (opens new window)

var addTwoNumbers = function(l1, l2) {
  let res = new ListNode();
  let carry = 0;
  let cur = res;
  while (l1 || l2 || carry) {
    const val1 = l1 ? l1.val : 0;
    const val2 = l2 ? l2.val : 0;
    const sum = val1 + val2 + carry;
    carry = sum >= 10 ? 1 : 0;
    cur.next = new ListNode(sum % 10);
    cur = cur.next;
    if (l1) {
      l1 = l1.next;
    }
    if (l2) {
      l2 = l2.next;
    }
  }
  return res.next;
};

删除排序链表中的重复元素

题目地址 (opens new window)

var deleteDuplicates = function(head) {
  if (!head || !head.next) {
    return head;
  }
  let cur = head;
  while (cur.next) {
    if (cur.val === cur.next.val) {
      cur.next = cur.next.next;
    } else {
      cur = cur.next;
    }
  }
  return head;
};

合并两个有序链表

题目地址 (opens new window)

var mergeTwoLists = function(l1, l2) {
  if (l1 === null) {
    return l2;
  } else if (l2 === null) {
    return l1;
  } else if (l1.val <= l2.val) {
    l1.next = mergeTwoLists(l1.next, l2);
    return l1;
  } else {
    l2.next = mergeTwoLists(l1, l2.next);
    return l2;
  }
};

var mergeTwoLists = function(l1, l2) {
  const dummy = new ListNode();
  let cur = dummy;
  while (l1 && l2) {
    if (l1.val <= l2.val) {
      cur.next = l1;
      l1 = l1.next;
    } else {
      cur.next = l2;
      l2 = l2.next;
    }
    cur = cur.next;
  }
  cur.next = l1 ? l1 : l2;
  return dummy.next;
};

合并 K 个升序链表

题目地址 (opens new window)

const merge2Lists = (l1, l2) => {
  const dummy = new ListNode();
  let cur = dummy;
  while (l1 && l2) {
    if (l1.val <= l2.val) {
      cur.next = l1;
      l1 = l1.next;
    } else {
      cur.next = l2;
      l2 = l2.next;
    }
    cur = cur.next;
  }
  cur.next = l1 ? l1 : l2;
  return dummy.next;
};

var mergeKLists = function(lists) {
  let res = null;
  for (let i = 0; i < lists.length; i++) {
    res = merge2Lists(res, lists[i]);
  }
  return res;
};

字典

字典的概念和用途

• 字典是以键值对的形式存储的。

• JavaScript 中的 Object 类就是以字典的形式设计的。

字典的代码实现

function Dictionary() {
  this.dataStore = new Array();
  this.add = add;
  this.find = find;
  this.remove = remove;
  this.count = count;
  this.clear = clear;
  this.showAll = showAll;
}

// 向字典中添加元素
function add(key, value) {
  this.dataStore[key] = value;
}

// 查询字典中的某个元素
function find(key) {
  return this.dataStore[key];
}

// 删除字典中的某个元素
function remove(key) {
  delete this.dataStore[key];
}

// 查询字典中的元素个数
function count() {
  return Object.keys(this.dataStore).length;
}

// 清空字典
function clear() {
  var dataKeys = Object.keys(this.dataStore);
  for (var key in dataKeys) {
    delete this.dataStore[dataKeys[key]];
  }
}

// 打印整个字典信息
function showAll() {
  var dataKeys = Object.keys(this.dataStore);
  for (var key in dataKeys) {
    console.log(dataKeys[key] + " -> " + this.dataStore[dataKeys[key]]);
  }
}

var goods = new Dictionary();
goods.add("first", 456);
goods.add("second", 145);
goods.add("third", 954);
console.log(goods.find("second"));
goods.showAll();
console.log(goods.count());
goods.remove("second");
goods.showAll();
goods.clear();
console.log(goods.count());

字典的另一种实现

var Dictionary = function() {
  var items = {};

  // 检查键是否存在
  this.has = function(key) {
    // return items.hasOwnProperty(key)
    return key in items;
  };

  this.set = function(key, value) {
    items[key] = value;
  };

  this.delete = function(key) {
    if (this.has(key)) {
      delete items[key];
      return true;
    }
    return false;
  };

  this.get = function(key) {
    if (this.has(key)) {
      return items[key];
    }
    return undefined;
  };

  this.getItems = function() {
    return items;
  };
};

散列

散列的概念和用途

• 散列后的数据可以快速插入取用。

• 在散列表上插入、删除和取用数据非常快，但是查找数据却效率低下，比如查找一组数据中的最大值和最小值。

• JavaScript 散列表基于数组设计，理想情况下散列函数会将每一个键值映射为唯一的数组索引，数组长度有限制，更现实的策略是将健均匀分布。

散列的一些关键点

• 数组长度是预先设定的，可以随时增加，所有元素根据和该元素对应的健，保存在数组的特定位置。

• 即使使用高效的散列函数，仍然存在两个键值相同的情况，这种现象称为碰撞。

• 数组的长度应该是一个质数，所有的策略都基于碰撞。

• 解决散列冲突的方法有：

  • 开链法：两个键相同保存位置一样。开辟第二个数组，也称第二个数组为链。

  • 线性探测法属于开放寻址散列，查找散列位置，如果当前位置没有继续寻找下一个位置。存储数据较大比较合适。数据大小 >= 1.5*数据（开链法），数据大小 >= 2*数据（线性探测法）。

• 更好的散列函数：djb2。

var djb2HashCode = function(key) {
  var hash = 5381;
  for (var i = 0; i < key.length; i++) {
    hash = hash * 33 + key.charCodeAt(i);
  }
  return hash % 1013;
};

散列的代码实现

function HashTable() {
  this.table = new Array(137);
  this.simpleHash = simpleHash;
  this.betterHash = betterHash;
  this.buildChains = buildChains;
  this.put = put;
  this.get = get;
  this.showHashTable = showHashTable;
}

// 简单的散列函数，使用除留余数法
function simpleHash(data) {
  var hash = 0;
  for (var i = 0; i < data.length; i++) {
    hash += data.charCodeAt(i);
  }
  return hash % this.table.length;
}

// 分布更均匀的散列函数
function betterHash(data) {
  var H = 31; // 质数
  var hash = 0;
  for (var i = 0; i < data.length; i++) {
    hash += H * hash + data.charCodeAt(i);
  }
  if (hash < 0) {
    hash += this.table.length - 1;
  }
  return hash % this.table.length;
}

// 开链法
function buildChains() {
  for (var i = 0; i < this.table.length; i++) {
    this.table[i] = new Array();
  }
}

// 插入数据
function put(data) {
  var pos = this.simpleHash(data);
  this.table[pos] = data;

  // var pos = this.betterHash(data);
  // this.table[pos] = data;

  // 开链法
  // var pos = this.simpleHash(data);
  // var index = 0;
  // if (!this.table[pos][index]) {
  //   this.table[pos][index] = data;
  //   index++;
  // } else {
  //   while (this.table[pos][index]) {
  //     index++;
  //   }
  //   this.table[pos][index] = data;
  // }

  // 线性探测法
  // var pos = this.simpleHash(data);
  // if (!this.table[pos]) {
  //   this.table[pos] = data;
  // } else {
  //   while (this.table[pos]) {
  //     pos++;
  //   }
  //   this.table[pos] = data;
  // }
}

// 取出数据
function get(data) {
  return this.table[this.simpleHash(data)];

  // 配合线性探测法
  // var pos = this.simpleHash(data);
  // console.log(data + '本来的位置是：' + pos);
  // for (var i = pos; i < this.table.length; i++) {
  //   if (this.table[i] === data) {
  //     return i;
  //   }
  // }
  // return -1;
}

// 打印整个散列表的数据
function showHashTable() {
  var n = 0;
  for (var i = 0; i < this.table.length; i++) {
    if (this.table[i]) {
      console.log("键 " + i + " 对应的值是：" + this.table[i]);
    }
  }

  // 配合开链法
  // var n = 0;
  // for (var i = 0; i < this.table.length; i++) {
  //   if (this.table[i][0]) {
  //     console.log('键 ' + i + ' 对应的值是：' + this.table[i]);
  //   }
  // }
}

var hashTable = new HashTable();

// 开链
// hashTable.buildChains();

hashTable.put("first");
hashTable.put("study");
hashTable.put("student");
hashTable.put("cool");
hashTable.put("ice");
hashTable.put("china");
hashTable.put("nicha");

// console.log('使用线性探测法之后 nicha 的位置是：' + hashTable.get('nicha'));

hashTable.showHashTable();

集合和哈希表

集合的概念和用途

• 集合是一种包含不同元素的数据结构。

• 在很多编程语言中并不把集合当成一种数据类型，当你想要创建一个数据结构，用来保存一段独一无二的文字的时候，集合就非常有用。

• 集合的成员是无序的。

• 集合中不允许相同成员存在。

集合的一些关键点

• 集合是一组无序但彼此间又有一定相关性的成员构成的，集合中的元素称为成员。

• 不包含任何成员的集合称为空集。全集则是包含一切可能成员的集合。

• 如果两个集合的成员完全相同，则称两个集合相等。

• 如果一个集合中的所有成员都属于另外一个集合，则前一集合称为后一集合的子集。

• 并集：将两个集合中的成员进行合并，得到一个新集合。

• 交集：两个集合中共同存在的成员组成一个新的集合。

• 差集：属于一个集合但不属于另一个集合的成员组成的集合。

集合的代码实现

function Set() {
  this.dataStore = [];
  this.add = add;
  this.remove = remove;
  this.has = has;
  this.size = size;
  this.show = show;
  this.union = union;
  this.intersect = intersect;
  this.difference = difference;
  this.subSet = subSet;
}

// 向集合中添加元素
function add(data) {
  if (!this.has(data)) {
    this.dataStore.push(data);
  }
}

// 删除集合中的元素
function remove(data) {
  var pos = this.dataStore.indexOf(data);
  if (pos !== -1) {
    this.dataStore.splice(pos, 1);
  }
}

// 判断集合中是否有某个元素
function has(data) {
  return this.dataStore.indexOf(data) > -1;
}

// 求集合中元素个数
function size() {
  return this.dataStore.length;
}

// 展示整个集合内容
function show() {
  return this.dataStore;
}

// 求并集
function union(set) {
  var tempSet = new Set();
  for (var i = 0; i < this.dataStore.length; i++) {
    tempSet.add(this.dataStore[i]);
  }
  for (var i = 0; i < set.dataStore.length; i++) {
    if (!tempSet.has(set.dataStore[i])) {
      tempSet.add(set.dataStore[i]);
    }
  }
  return tempSet;
}

// 求交集
function intersect(set) {
  var tempSet = new Set();
  for (var i = 0; i < this.dataStore.length; i++) {
    if (set.has(this.dataStore[i])) {
      tempSet.add(this.dataStore[i]);
    }
  }
  return tempSet;
}

// 求差集
function difference(set) {
  var tempSet = new Set();
  for (var i = 0; i < this.dataStore.length; i++) {
    if (!set.has(this.dataStore[i])) {
      tempSet.add(this.dataStore[i]);
    }
  }
  return tempSet;
}

// 判断一个集合是否是另一个集合的子集
function subSet(set) {
  if (set.size() > this.size()) {
    return false;
  } else {
    for (var i = 0; i < set.dataStore.length; i++) {
      if (!this.has(set.dataStore[i])) {
        return false;
      }
    }
    return true;
  }
}

var set = new Set();
set.add("first");
set.add("second");
set.add("third");
// set.remove('first');
var set1 = new Set();
set1.add("first");
set1.add("second");
set1.add("fourth");
console.log(set.show());
console.log("并集：", set.union(set1).show());
console.log("交集：", set.intersect(set1).show());
console.log("差集：", set.difference(set1).show());
var set2 = new Set();
set1.add("first");
set1.add("second");
console.log("是否是子集：", set.subSet(set2));

集合的另一种实现

var Set = function() {
  var items = {};

  // has 检查元素是否存在
  this.has = function(value) {
    return items.hasOwnProperty(value);
  };

  // add 添加元素，要注意集合具有不重复性
  this.add = function(value) {
    if (!this.has(value)) {
      // 对象有两种访问方式：点语法和方括号语法，点语法后面的键不能是变量，只能是对象名；但是方括号语法可以是变量
      items[value] = value;
      return value;
    }
    return false;
  };

  // 移除元素
  this.remove = function(value) {
    if (this.has(value)) {
      delete items[value];
      return true;
    } else {
      return false;
    }
  };

  // 清空集合
  this.clear = function() {
    items = {};
  };

  // 获取集合的大小
  this.size = function() {
    // 遍历集合
    // var count = 0;
    // for(var i in items){
    //     if(items.hasOwnProperty(i)){     // 判断对象是否包含特定的自身属性（非继承）
    //         count++;
    //     }
    // }
    // return count;

    return Object.keys(items).length; // 静态方法Object.keys()返回的是一个数组，数组里的元素是键名，es6提出来的
  };

  // 提取集合的全部值并以数组形式返回
  this.value = function() {
    var values = [];
    for (var i in items) {
      if (items.hasOwnProperty(i)) {
        values.push(items[i]);
      }
    }
    return values;
  };

  // 并集
  this.union = function(otherSet) {
    var resultSet = new Set();

    // 把自己的值提取出来
    var arr = this.value();
    for (var i = 0; i < arr.length; i++) {
      resultSet.add(arr[i]);
    }

    // 把另一个集合的值提取出来
    arr = otherSet.value();
    for (var i = 0; i < arr.length; i++) {
      resultSet.add(arr[i]);
    }
    return resultSet;
  };

  // 交集
  this.intersection = function(otherSet) {
    var resultSet = new Set();

    // 把自己的值提取出来
    var arr = this.value();
    for (var i = 0; i < arr.length; i++) {
      if (otherSet.has(arr[i])) {
        resultSet.add(arr[i]);
      }
    }
    return resultSet;
  };

  // 差集
  this.difference = function(otherSet) {
    var resultSet = new Set();
    var arr = this.value();
    for (var i = 0; i < arr.length; i++) {
      if (!otherSet.has(arr[i])) {
        resultSet.add(arr[i]);
      }
    }
    return resultSet;
  };

  // 获取整个集合
  this.getItems = function() {
    return items;
  };
};

HashMap、TreeMap、HashSet、TreeSet

• Hash 和 Binary Search Tree 是 Map 和 Set 底层实现的两种方式。

• HashMap 和 HashSet 效率更快，但是元素是乱序的；而 TreeMap 和 TreeSet 效率相对慢一点，但是元素是有序的。所以具体使用哪种要看具体的需求场景。

两数之和

题目地址 (opens new window)

var twoSum = function(nums, target) {
  const map = new Map();
  for (let i = 0; i < nums.length; i++) {
    const diff = target - nums[i];
    if (map.has(diff)) {
      return [map.get(diff), i];
    }
    map.set(nums[i], i);
  }
  return [];
};

两个数组的交集

题目地址 (opens new window)

// 两个集合，时间和空间复杂度都是 O(m+n)
var intersection = function(nums1, nums2) {
  const set1 = new Set(nums1);
  const res = [];
  for (const num of nums2) {
    if (set1.has(num)) {
      res.push(num);
      set1.delete(num);
    }
  }
  return res;
};

// 排序+双指针，时间复杂度是 O(mlogm+nlogn)，空间复杂度是 O(logm+logn)
var intersection = function(nums1, nums2) {
  nums1.sort((a, b) => a - b);
  nums2.sort((a, b) => a - b);
  const len1 = nums1.length;
  const len2 = nums2.length;
  const res = [];
  let i = 0;
  let j = 0;
  while (i < len1 && j < len2) {
    if (nums1[i] === nums2[j]) {
      if (!res.includes(nums1[i])) {
        res.push(nums1[i]);
      }
      i++;
      j++;
    } else if (nums1[i] < nums2[j]) {
      i++;
    } else {
      j++;
    }
  }
  return res;
};

赎金信

题目地址 (opens new window)

var canConstruct = function(ransomNote, magazine) {
  if (ransomNote.length > magazine.length) {
    return false;
  }

  const charArr = new Array(26).fill(0);
  const baseCharCode = "a".charCodeAt();

  for (const c of magazine) {
    charArr[c.charCodeAt() - baseCharCode]++;
  }
  for (const c of ransomNote) {
    charArr[c.charCodeAt() - baseCharCode]--;
    if (charArr[c.charCodeAt() - baseCharCode] < 0) {
      return false;
    }
  }

  return true;
};

有效的字母异位词

题目地址 (opens new window)

方法一：可以直接将两个字符串中的字符进行排序，然后比较排序后的结果是不是完全一样。时间复杂度为：O(nlogn)。

var isAnagram = function(s, t) {
  return (
    s.length === t.length && [...s].sort().join("") === [...t].sort().join("")
  );
};

方法二：使用 map 来存储两个字符串中每个字符的出现的次数，然后比较这两个 map 是否一致。时间复杂度为：O(n)。

方法三：使用哈希表，思路跟使用 map 类似，维护一个长度为 26 的数组，先遍历记录字符串 s 中每个字符出现的次数，然后在遍历字符串 t，减去数组中相应字符的次数。遍历结束后，如果数组中有某一位次数不为 0，说明两者不一致，返回 false。时间复杂度为：O(n)。

charCodeAt 和 codePointAt 的作用都是获取字符的 Unicode 编码值，区别就是前者只能处理 16 位二进制数 0xffff 以内的值，而后者能正确处理到 32 位二进制数。

var isAnagram = function(s, t) {
  if (s.length !== t.length) {
    return false;
  }

  const arr = new Array(26).fill(0);
  const baseCodePoint = "a".codePointAt(0);

  for (let i = 0; i < s.length; i++) {
    arr[s.codePointAt(i) - baseCodePoint]++;
  }
  for (let i = 0; i < t.length; i++) {
    arr[t.codePointAt(i) - baseCodePoint]--;
    if (arr[t.codePointAt(i) - baseCodePoint] < 0) {
      return false;
    }
  }

  return true;
};

字母异位词分组

题目地址 (opens new window)

// 由于互为字母异位词的两个字符串包含的字母相同，因此对两个字符串分别进行排序之后得到的字符串一定是相同的，故可以将排序之后的字符串作为哈希表的键
var groupAnagrams = function(strs) {
  const map = new Map();
  for (const str of strs) {
    const arr = Array.from(str);
    arr.sort();
    const key = arr.toString();
    const value = map.get(key) ? map.get(key) : [];
    value.push(str);
    map.set(key, value);
  }
  return Array.from(map.values());
};

存在重复元素

题目地址 (opens new window)

var containsDuplicate = function(nums) {
  const set = new Set();
  for (let i = 0; i < nums.length; i++) {
    if (set.has(nums[i])) {
      return true;
    }
    set.add(nums[i]);
  }
  return false;
};

// 另一种解法，先排序，排序后重复的元素肯定位于相邻的位置
var containsDuplicate = function(nums) {
  nums.sort((a, b) => a - b);
  for (let i = 0; i < nums.length - 1; i++) {
    if (nums[i] === nums[i + 1]) {
      return true;
    }
  }
  return false;
};

缺失的第一个正数

题目地址 (opens new window)

// 将给定的数组设计成哈希表，将所有在 [1,N] 范围内的数放入哈希表
var firstMissingPositive = function(nums) {
  const n = nums.length;
  // 将数组中小于等于 0 的数修改成任意一个大于 n 的数，比如 n + 1
  // 这样一来，数组中的所有数就都是正数了，方便后续将「标记」表示为「负号」
  for (let i = 0; i < n; i++) {
    if (nums[i] <= 0) {
      nums[i] = n + 1;
    }
  }
  // 遍历数组中的每一个数 x，它可能已经被打了标记，因此原本对应的数为 ∣x∣
  // 如果 |x|∈[1, n]，那么我们给数组中的第 ∣x∣−1 个位置的数添加一个负号
  // 如果它已经有负号，不需要重复添加
  for (let i = 0; i < n; i++) {
    const x = Math.abs(nums[i]);
    if (x >= 1 && x <= n) {
      nums[x - 1] = nums[x - 1] < 0 ? nums[x - 1] : -nums[x - 1];
    }
  }
  // 上面的工作做完之后，如果数组中的每一个数都是负数，那么答案是 N+1，否则答案是第一个正数的位置加 1
  for (let i = 0; i < n; i++) {
    if (nums[i] > 0) {
      return i + 1;
    }
  }
  return n + 1;
};

LRU 缓存

题目地址 (opens new window)

var LRUCache = function(capacity) {
  this.map = new Map();
  this.capacity = capacity;
};

LRUCache.prototype.get = function(key) {
  if (!this.map.has(key)) {
    return -1;
  }
  const value = this.map.get(key);
  this.map.delete(key);
  this.map.set(key, value);
  return value;
};

LRUCache.prototype.put = function(key, value) {
  if (this.map.has(key)) {
    this.map.delete(key);
  }
  this.map.set(key, value);
  if (this.map.size > this.capacity) {
    this.map.delete(this.map.keys().next().value);
  }
};

单词替换

题目地址 (opens new window)

var replaceWords = function(dictionary, sentence) {
  const set = new Set();
  for (const root of dictionary) {
    set.add(root);
  }
  const words = sentence.split(" ");
  for (let i = 0; i < words.length; i++) {
    const word = words[i];
    for (let j = 0; j < word.length; j++) {
      if (set.has(word.substring(0, j + 1))) {
        words[i] = word.substring(0, j + 1);
        break;
      }
    }
  }
  return words.join(" ");
};

树

二叉树的概念和用途

• 树是一种非线性的数据结构，分层存储。

• 树被用来存储具有层级关系的数据，还被用来存储有序列表。

• 二叉树进行查找特别快，为二叉树添加或删除元素也特别快。

二叉树的一些关键点

• 树由一组以边连接的节点组成。

• 一棵树最上面的节点称为根节点，如果一个节点下面连接多个节点，那么该节点称为父节点，它下面的节点被称为子节点。一个节点可以有 0 个、1 个或多个子节点。没有任何子节点的节点称为叶子节点。

• 二叉树是一种特殊的树，子节点数不超过两个。

• 从一个节点走到另一个节点的这一组边称为路径。

• 以某种特定顺序访问树中的所有节点称为树的遍历。

• 树分为几个层次，根节点是第 0 层，它的子节点第 1 层，以此类推。我们定义树的层数就是树的深度。

• 每个节点都有一个与之相关的值，该值有时被称为键。

• 一个父节点的两个子节点分别称为左节点和右节点。

二叉搜索树

二叉搜索树又称有序二叉树、排序二叉树，它具有以下性质：

• 左子树上所有节点的值均小于它的根节点的值；

• 右子树上所有节点的值均大于它的根节点的值；

• 左右子树也是二叉搜索树。

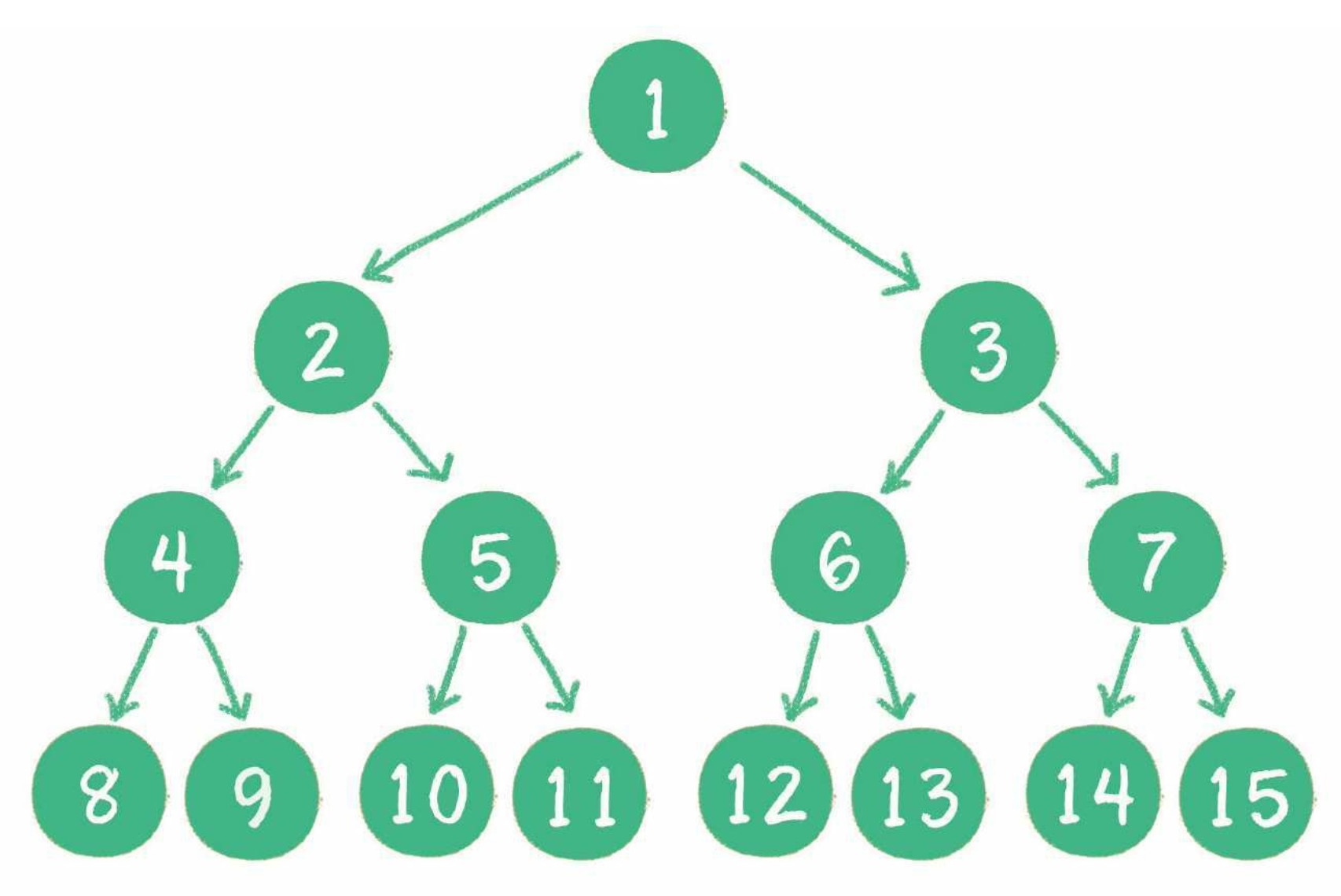
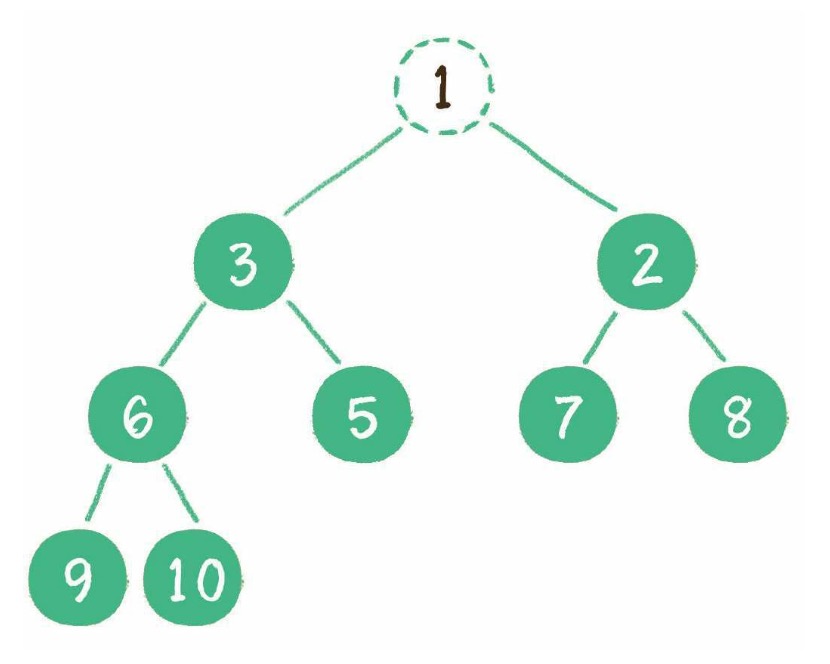
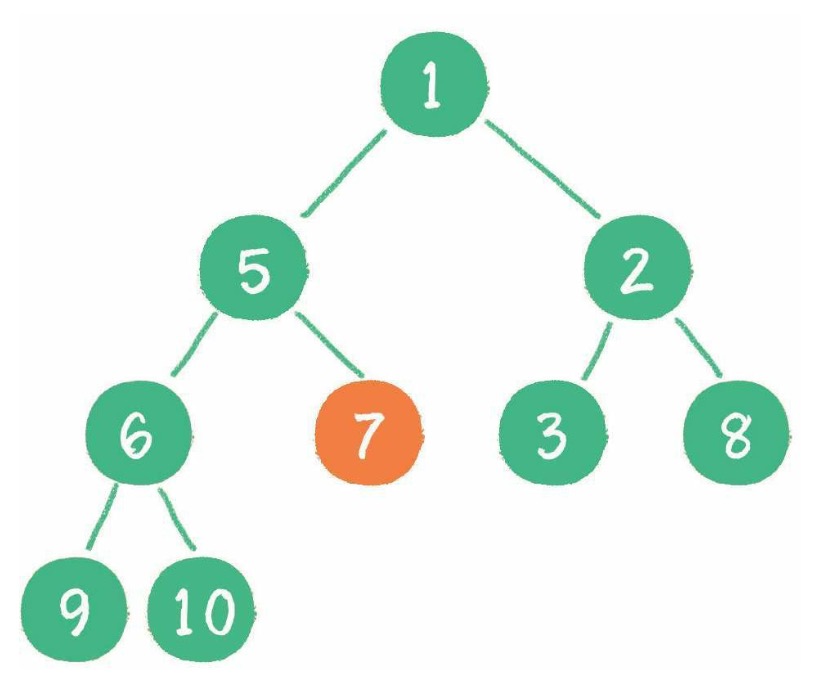
满二叉树和完全二叉树

• 一个二叉树的所有非叶子节点都存在左右孩子，并且所有叶子节点都在同一层级上，那么这个树就是满二叉树。

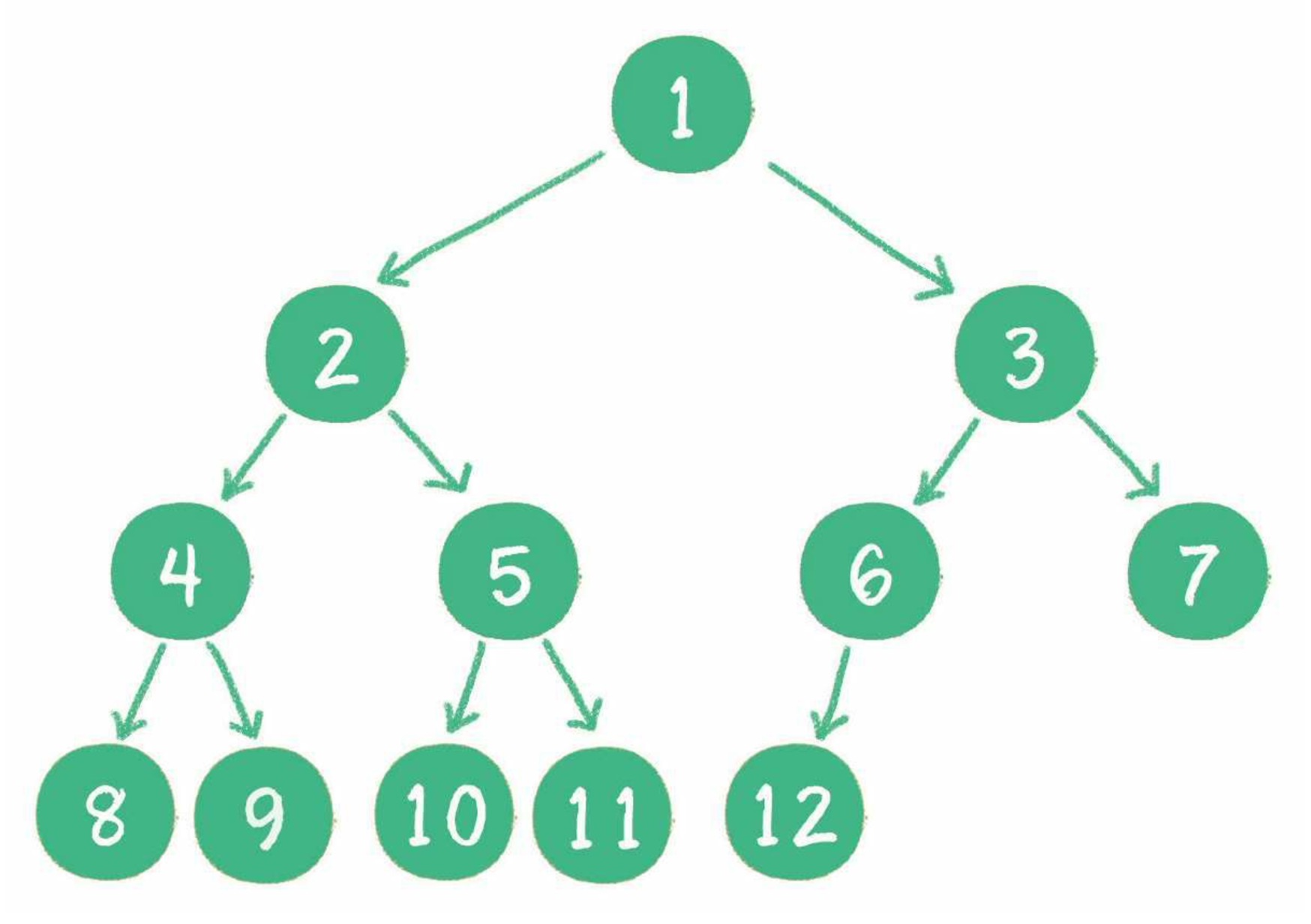
• 对一个有 n 个节点的二叉树，按层级顺序编号，则所有节点的编号为从 1 到 n。如果这个树所有节点和同样深度的满二叉树的编号为从 1 到 n 的节点位置相同，则这个二叉树为完全二叉树。

在上图中，二叉树编号从 1 到 12 的 12 个节点，和前面满二叉树编号从 1 到 12 的节点位置完全对应。因此这个树是完全二叉树。

完全二叉树的条件没有满二叉树那么苛刻：满二叉树要求所有分支都是满的；而完全二叉树只需保证最后一个节点之前的节点都齐全即可。

二叉树的存储方式

📌 1. 链式存储结构

链式存储是二叉树最直观的存储方式。

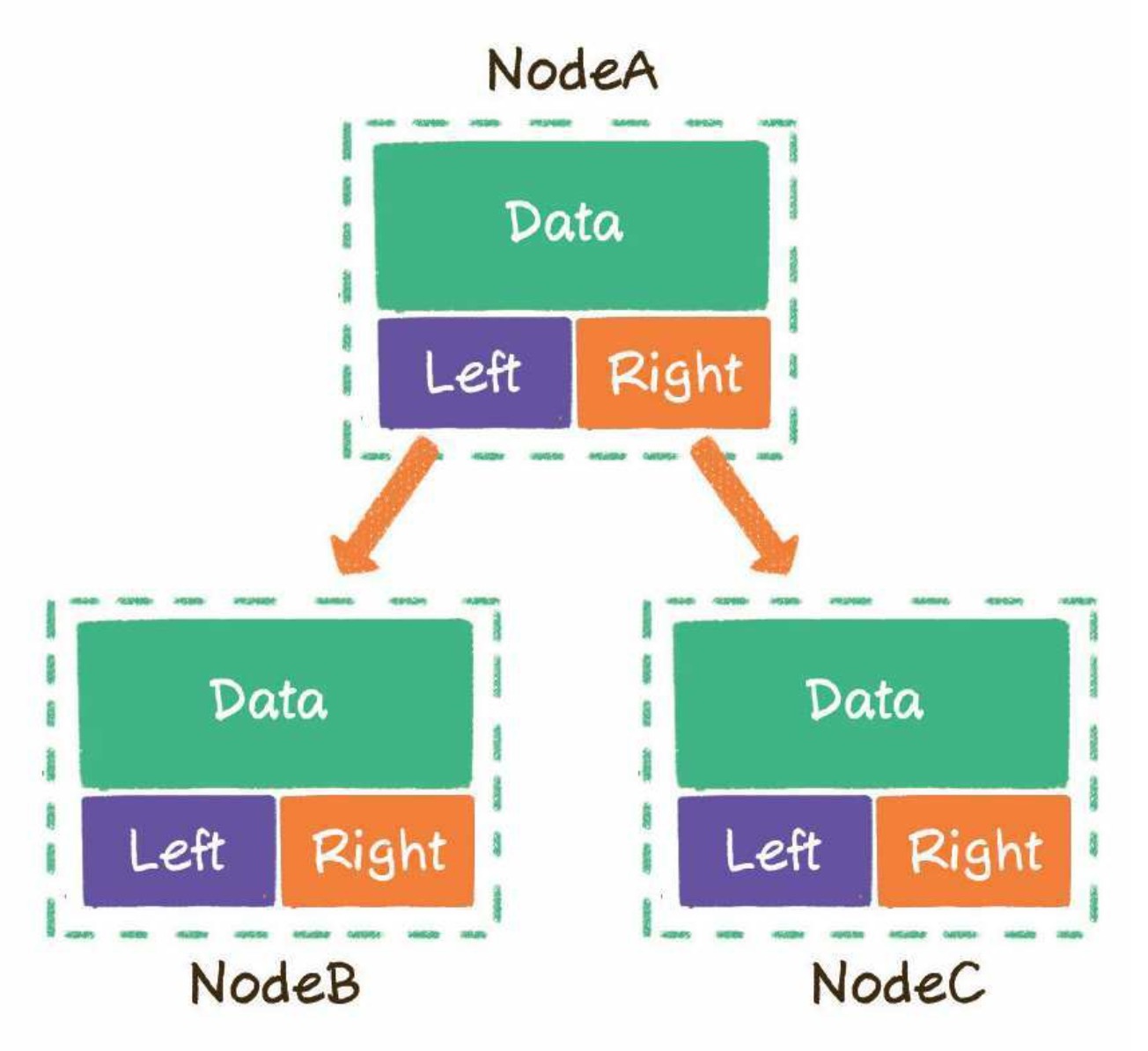
二叉树中一个节点最多可以指向左右两个孩子节点，所以二叉树的每一个节点包含 3 部分。

• 存储数据的 data 变量

• 指向左孩子的 left 指针

• 指向右孩子的 right 指针

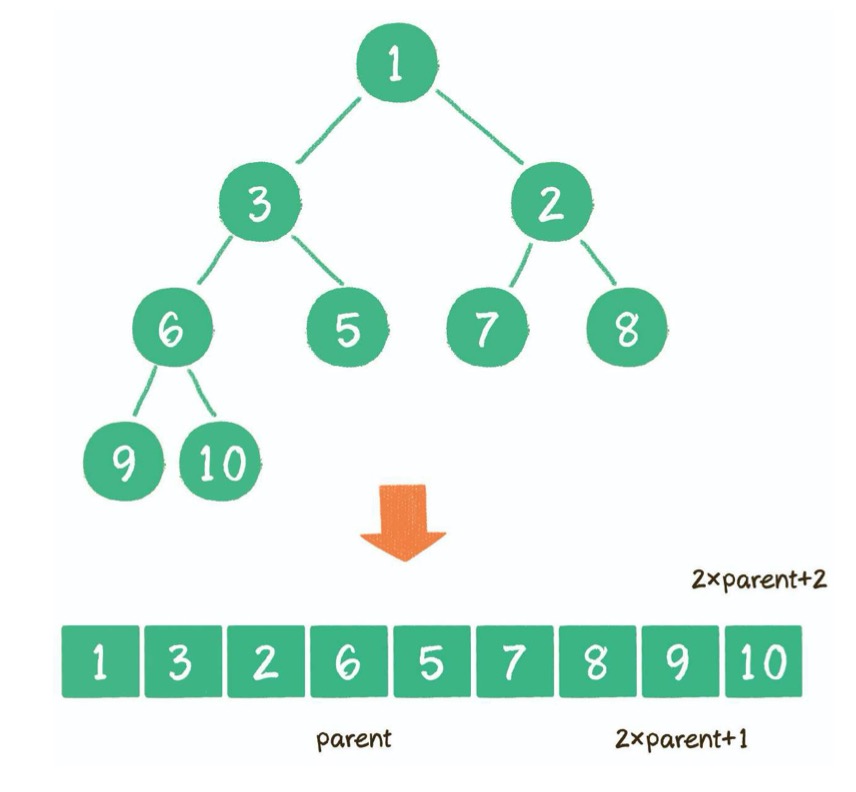
📌 2. 数组

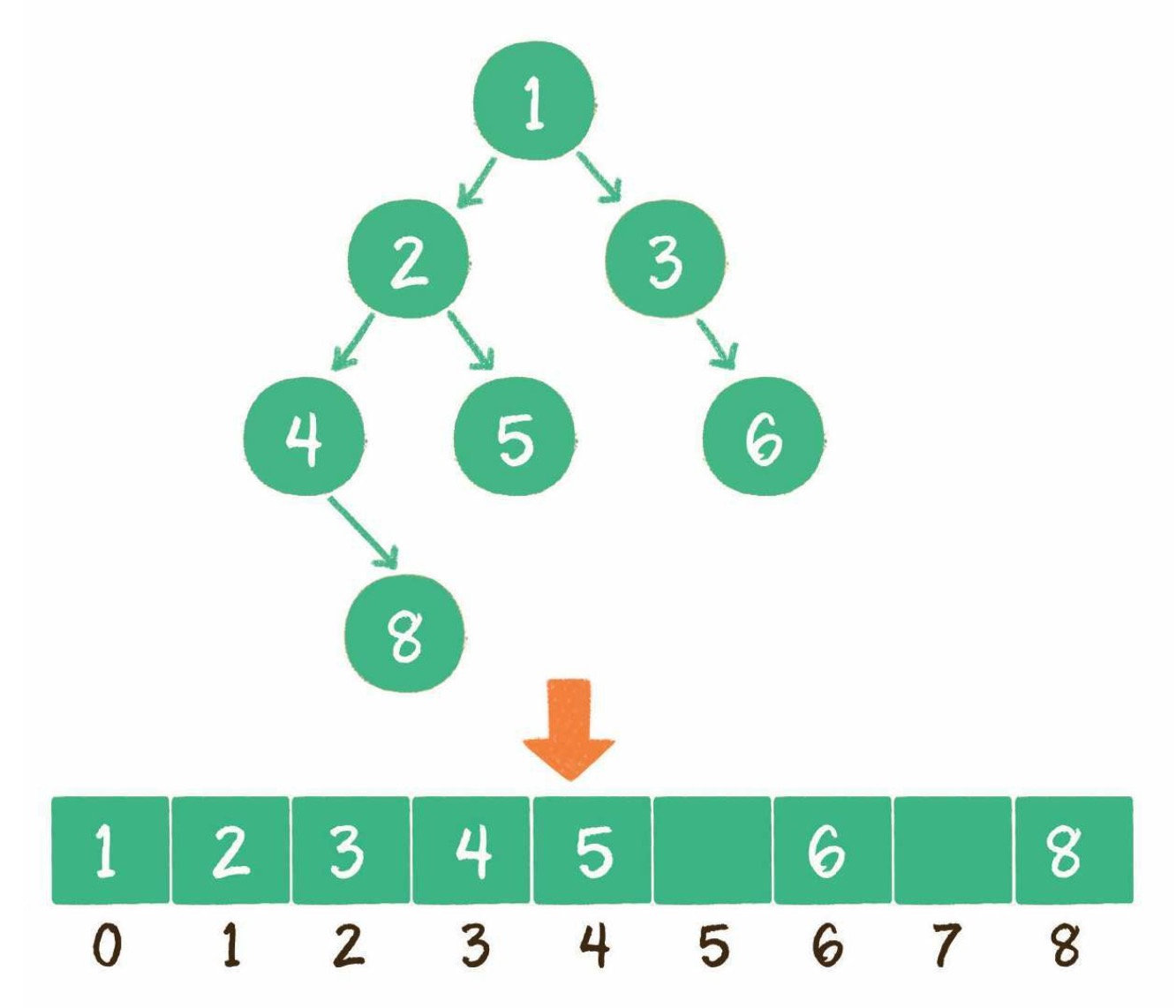
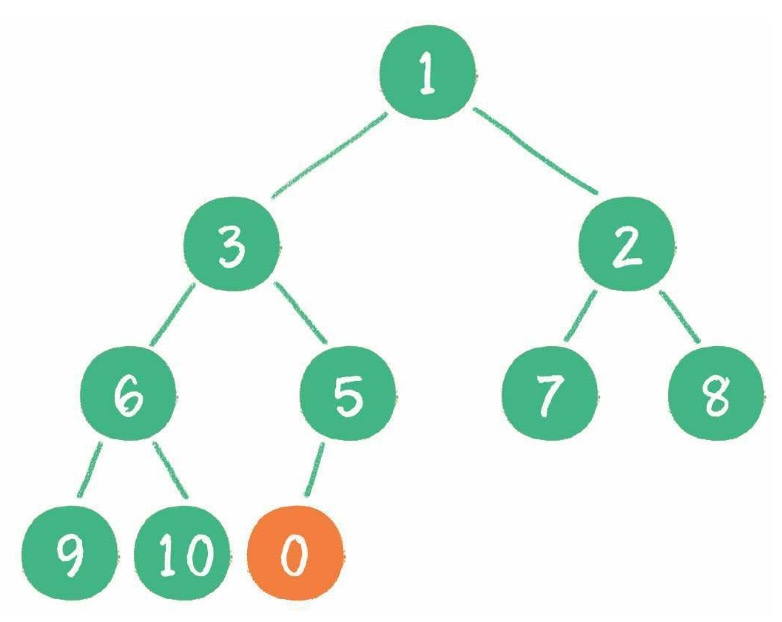
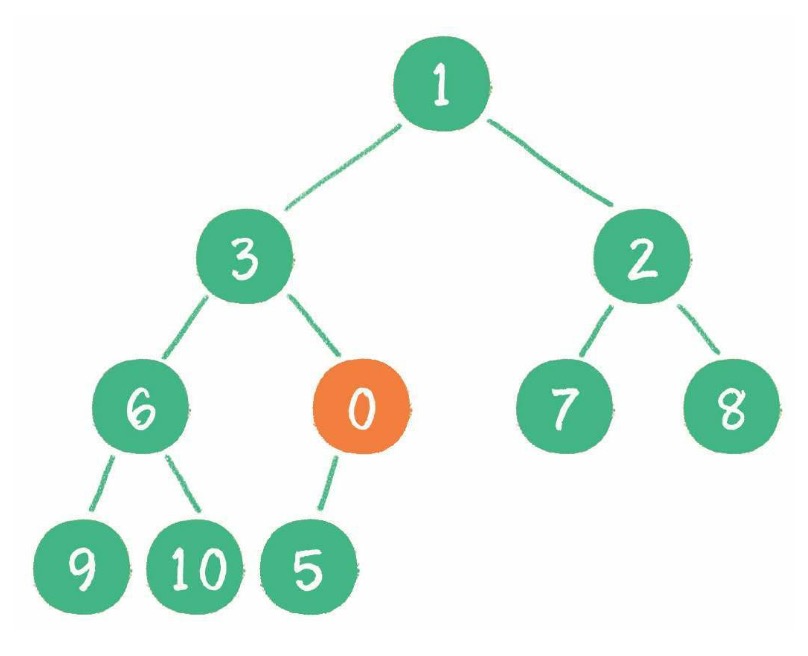
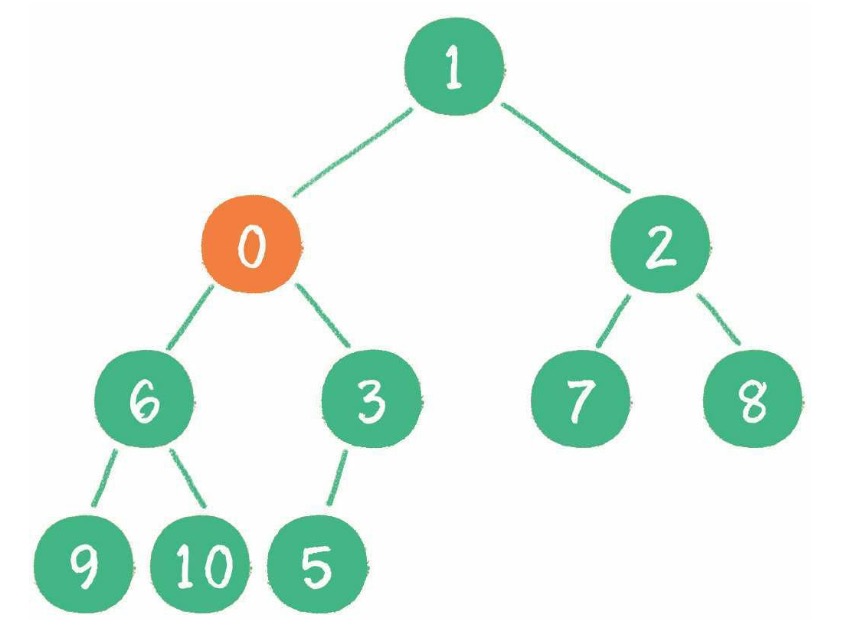
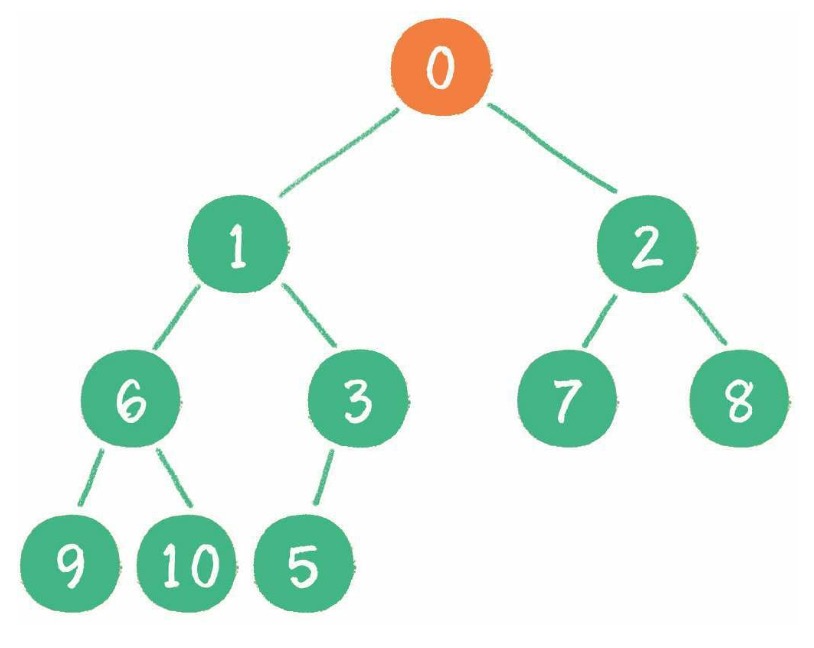
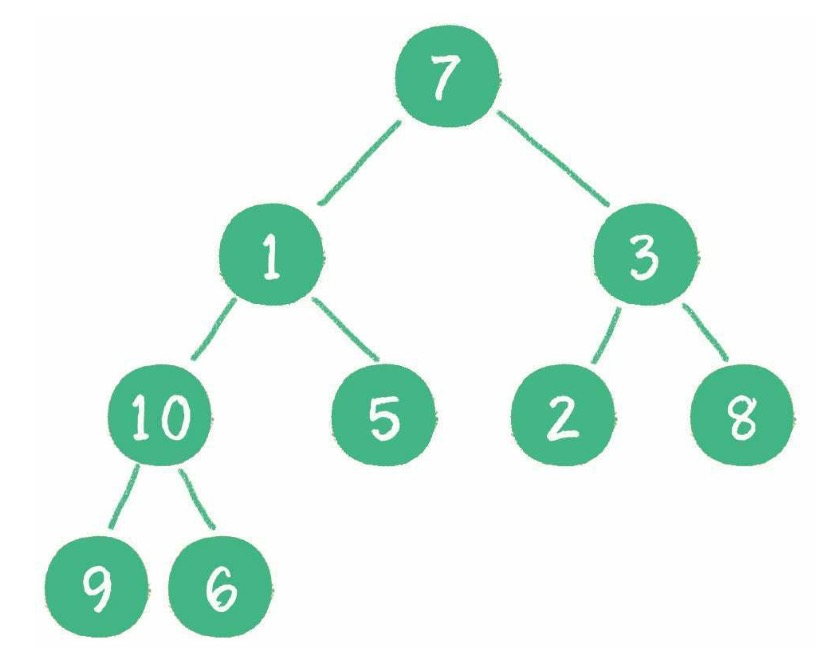
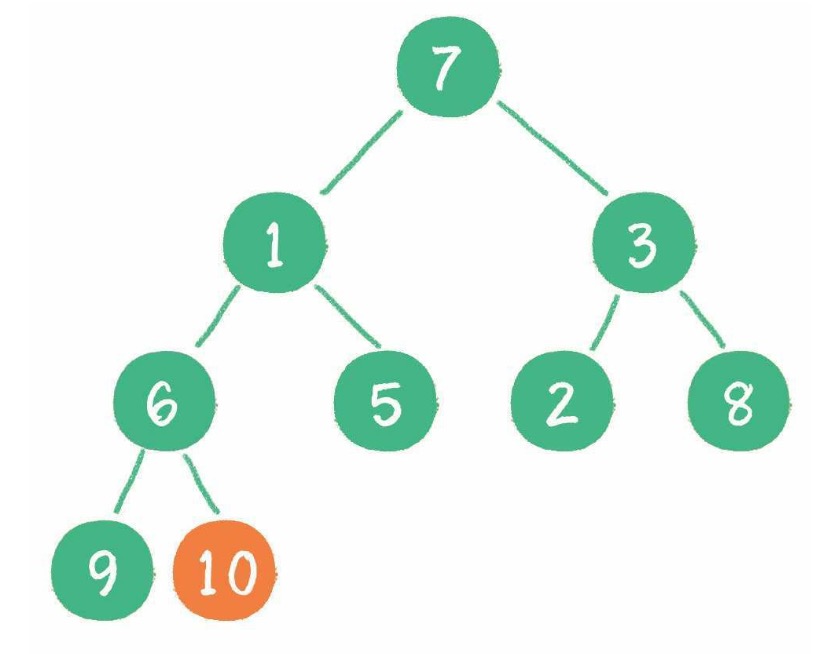
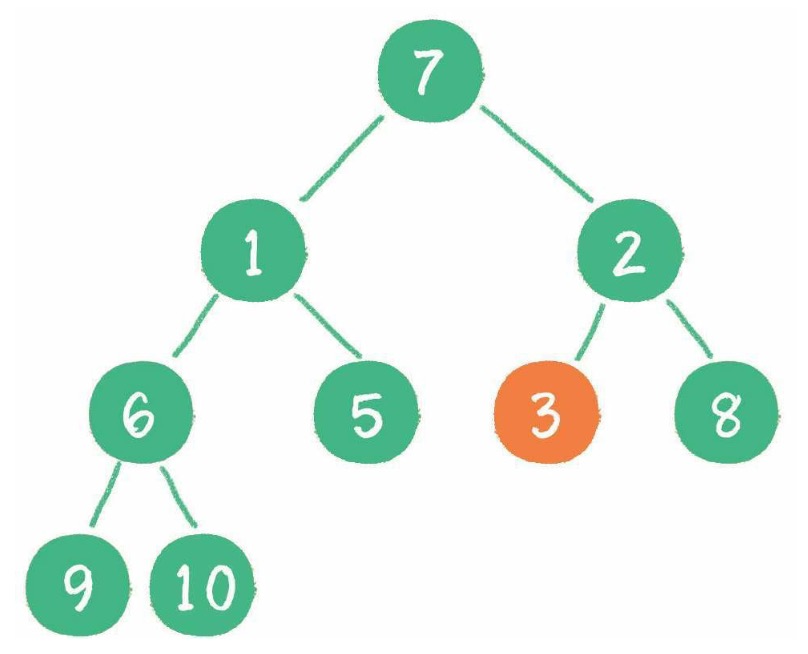
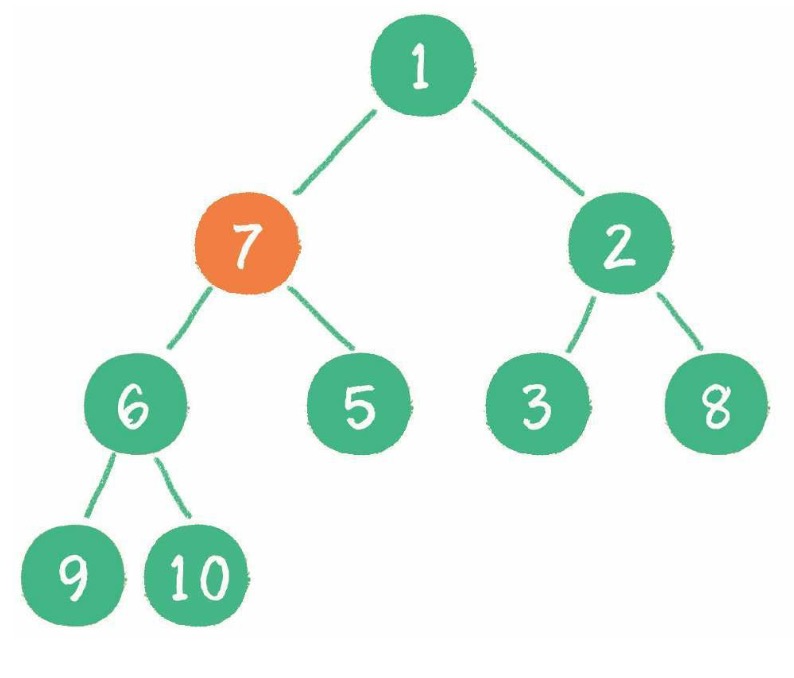
使用数组存储时，会按照层级顺序把二叉树的节点放到数组中对应的位置上。如果某一个节点的左孩子或右孩子空缺，则数组的相应位置也空出来。

为什么这样设计呢？因为这样可以更方便地在数组中定位二叉树的孩子节点和父节点。

假设一个父节点的下标是 parent，那么它的左孩子节点下标就是 2 × parent + 1；右孩子节点下标就是 2 × parent + 2。

反过来，假设一个左孩子节点的下标是 leftChild，那么它的父节点下标就是 (leftChild-1)/ 2。

假如节点 4 在数组中的下标是 3，节点 4 是节点 2 的左孩子，节点 2 的下标可以直接通过计算得出。

节点 2 的下标 = (3-1)/2 = 1

显然，对于一个稀疏的二叉树来说，用数组表示法是非常浪费空间的。

什么样的二叉树最适合用数组表示呢?

二叉堆，一种特殊的完全二叉树，就是用数组来存储的。

二叉树的代码实现

// 节点
function Node(data) {
  this.data = data;
  this.left = null;
  this.right = null;
}

// 二叉搜索树
function Bst() {
  this.root = null;
  this.insert = insert;
  this.preOrder = preOrder;
  this.inOrder = inOrder;
  this.lastOrder = lastOrder;
  this.iteratePreOrder = iteratePreOrder;
  this.iterateInOrder = iterateInOrder;
  this.iterateLastOrder = iterateLastOrder;
  this.getMin = getMin;
  this.getMax = getMax;
  this.find = find;
  this.remove = remove;
}

// 向树中插入数据
function insert(data) {
  var node = new Node(data);
  if (this.root === null) {
    this.root = node;
  } else {
    var current = this.root;
    var parent;
    while (true) {
      parent = current;
      if (data < current.data) {
        current = current.left;
        if (current === null) {
          parent.left = node;
          break;
        }
      } else {
        current = current.right;
        if (current === null) {
          parent.right = node;
          break;
        }
      }
    }
  }
}

/* 插入操作也可以这么写 */
// 向树中插入数据
function insert(data) {
  var newNode = new Node(data); // 新节点
  if (this.root === null) {
    this.root = newNode;
  } else {
    insertNode(this.root, newNode);
  }
}
// 插入节点方法
function insertNode(node, newNode) {
  if (newNode.data > node.data) {
    // 往右走
    if (node.right === null) {
      node.right = newNode;
    } else {
      insertNode(node.right, newNode); // 递归
    }
  } else if (newNode.data < node.data) {
    // 往左走
    if (node.left === null) {
      node.left = newNode;
    } else {
      insertNode(node.left, newNode); // 递归
    }
  }
}

// 前序遍历：根->左->右
function preOrder(node, res) {
  if (node) {
    res.push(node.data);
    preOrder(node.left, res);
    preOrder(node.right, res);
  }
  return res;
}

// 中序遍历：左->根->右
function inOrder(node, res) {
  if (node) {
    inOrder(node.left, res);
    res.push(node.data);
    inOrder(node.right, res);
  }
  return res;
}

// 后序遍历：左->右->根
function lastOrder(node, res) {
  if (node) {
    lastOrder(node.left, res);
    lastOrder(node.right, res);
    res.push(node.data);
  }
  return res;
}

// 前序遍历的迭代实现
function iteratePreOrder(node, res) {
  const stack = [];
  while (node || stack.length) {
    // 迭代访问节点的左孩子，并入栈
    while (node) {
      res.push(node.data);
      stack.push(node);
      node = node.left;
    }
    // 如果节点没有左孩子，则弹出栈顶节点，访问节点右孩子
    if (stack.length) {
      node = stack.pop();
      node = node.right;
    }
  }
  return res;
}

// 中序遍历的迭代实现
function iterateInOrder(node, res) {
  const stack = [];
  while (node || stack.length) {
    // 迭代访问节点的左孩子，并入栈
    while (node) {
      stack.push(node);
      node = node.left;
    }
    // 如果节点没有左孩子，则弹出栈顶节点，访问节点右孩子
    if (stack.length) {
      node = stack.pop();
      res.push(node.data);
      node = node.right;
    }
  }
  return res;
}

// 后序遍历的迭代实现
function iterateLastOrder(node, res) {
  const stack = [];
  let prev = null;
  while (node || stack.length) {
    while (node) {
      stack.push(node);
      node = node.left;
    }
    node = stack.pop();
    if (node.right === null || node.right === prev) {
      res.push(node.data);
      prev = node;
      node = null;
    } else {
      stack.push(node);
      node = node.right;
    }
  }
  return res;
}

// 获取树中的最小节点
function getMin(node) {
  var current = this.root || node;
  while (current.left) {
    current = current.left;
  }
  return current;
}

// 获取树中的最大节点
function getMax(node) {
  var current = this.root || node;
  while (current.right) {
    current = current.right;
  }
  return current;
}

// 查找某个数据
function find(data) {
  var current = this.root;
  while (current) {
    if (data === current.data) {
      return current;
    } else if (data < current.data) {
      current = current.left;
    } else {
      current = current.right;
    }
  }
  return null;
}

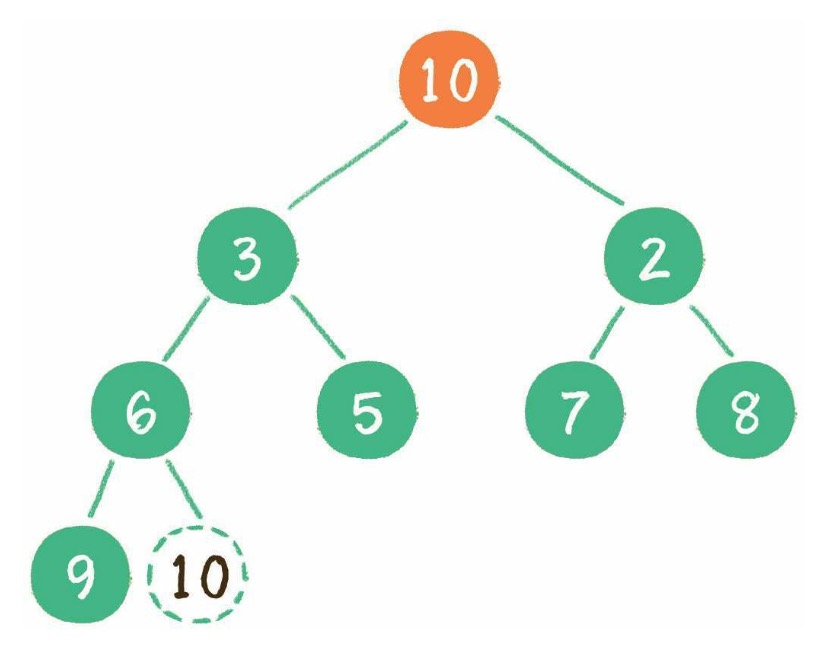
// 删除某个数据
function remove(data) {
  removeNode(this.root, data);
}

// 删除节点方法
function removeNode(node, data) {
  if (node === null) {
    return null;
  }
  if (data === node.data) {
    // 叶子节点
    if (node.left === null && node.right === null) {
      return null;
    }
    // 只有右节点
    if (node.left === null) {
      return node.right;
    }
    // 只有左节点
    if (node.right === null) {
      return node.left;
    }
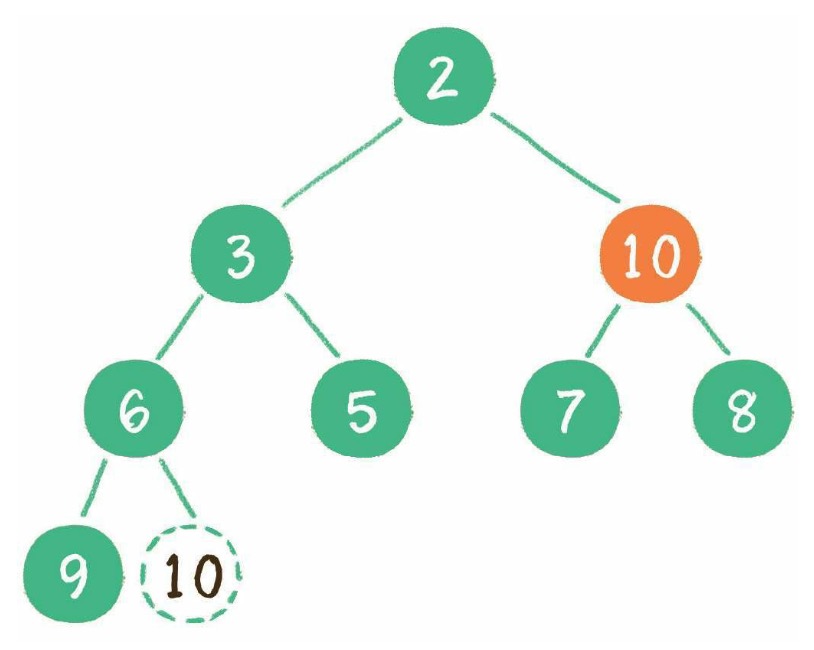
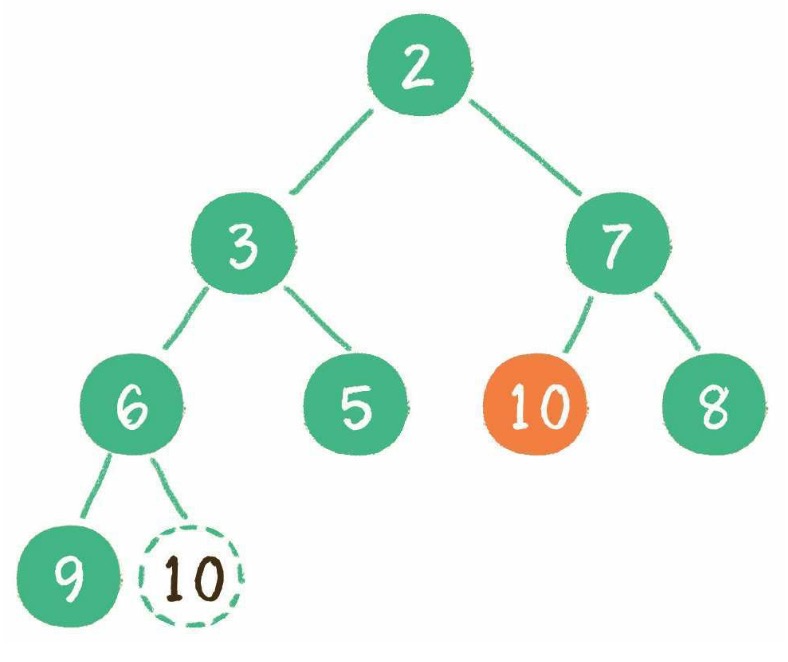
    // 左右节点都有，记住删除后要替换成右子树的最小节点
    var tempNode = getMin(node.right); // 找到右子树的最小节点
    node.data = tempNode.data;
    node.right = removeNode(node.right, tempNode.data);
    return node;
  } else if (data < node.data) {
    node.left = removeNode(node.left, data);
    return node;
  } else {
    node.right = removeNode(node.right, data);
    return node;
  }
}

var bst = new Bst();
bst.insert(23);
bst.insert(45);
bst.insert(16);
bst.insert(37);
bst.insert(3);
bst.insert(99);
bst.insert(22);
console.log("前序遍历：", bst.preOrder(bst.root, []));
console.log("中序遍历：", bst.inOrder(bst.root, []));
console.log("后序遍历：", bst.lastOrder(bst.root, []));
console.log("最小节点：", bst.getMin());
console.log("最大节点：", bst.getMax());
bst.remove(16);
console.log("中序遍历：", bst.inOrder(bst.root, []));

二叉树的前序遍历

题目地址 (opens new window)

// 递归解法
var preorderTraversal = function(root) {
  const res = [];
  const preOrder = (node) => {
    if (node) {
      res.push(node.val);
      preOrder(node.left);
      preOrder(node.right);
    }
  };
  preOrder(root);
  return res;
};

// 迭代解法，使用栈
var preorderTraversal = function(root) {
  if (root === null) return [];
  const res = [];
  const stack = [root];
  while (stack.length) {
    const node = stack.pop();
    res.push(node.val);
    if (node.right) {
      stack.push(node.right);
    }
    if (node.left) {
      stack.push(node.left);
    }
  }
  return res;
};

二叉树的中序遍历

题目地址 (opens new window)

// 递归解法
var inorderTraversal = function(root) {
  const res = [];
  const inOrder = (node) => {
    if (node) {
      inOrder(node.left);
      res.push(node.val);
      inOrder(node.right);
    }
  };
  inOrder(root);
  return res;
};

// 迭代解法，使用栈
var inorderTraversal = function(root) {
  const res = [];
  const stack = [];
  while (root || stack.length) {
    while (root) {
      stack.push(root);
      root = root.left;
    }
    root = stack.pop();
    res.push(root.val);
    root = root.right;
  }
  return res;
};

二叉树的后序遍历

题目地址 (opens new window)

// 递归解法
var postorderTraversal = function(root) {
  const res = [];
  const postOrder = (node) => {
    if (node) {
      postOrder(node.left);
      postOrder(node.right);
      res.push(node.val);
    }
  };
  postOrder(root);
  return res;
};

// 迭代解法
var postorderTraversal = function(root) {
  if (root === null) return [];
  const res = [];
  const queue = [root];
  while (queue.length) {
    const node = queue.pop();
    res.unshift(node.val);
    if (node.left) {
      queue.push(node.left);
    }
    if (node.right) {
      queue.push(node.right);
    }
  }
  return res;
};

二叉树的深度优先遍历

class TreeNode {
  constructor(val, left = null, right = null) {
    this.val = val;
    this.left = left;
    this.right = right;
  }
}

const root = new TreeNode(1);

root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);
root.right.left = new TreeNode(6);
root.right.right = new TreeNode(7);

const dfs = (node) => {
  if (node === null) {
    return;
  }
  console.log(node.val);
  dfs(node.left);
  dfs(node.right);
};

dfs(root); // 1 2 4 5 3 6 7

二叉树的广度优先遍历

class TreeNode {
  constructor(val, left = null, right = null) {
    this.val = val;
    this.left = left;
    this.right = right;
  }
}

const root = new TreeNode(1);

root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);
root.right.left = new TreeNode(6);
root.right.right = new TreeNode(7);

const bfs = (node) => {
  if (node === null) {
    return;
  }
  const queue = [node];
  while (queue.length) {
    const cur = queue.shift();
    console.log(cur.val);
    if (cur.left) {
      queue.push(cur.left);
    }
    if (cur.right) {
      queue.push(cur.right);
    }
  }
};

bfs(root); // 1 2 4 5 3 6 7

二叉树的最大深度

题目地址 (opens new window)

// 递归
var maxDepth = function(root) {
  if (root === null) return 0;
  const left = maxDepth(root.left);
  const right = maxDepth(root.right);
  return Math.max(left, right) + 1;
};

// 深度优先遍历
var maxDepth = function(root) {
  if (root === null) return 0;
  let depth = 0;
  const stack = [{ node: root, depth: 1 }];
  while (stack.length) {
    const { node, depth: curDepth } = stack.pop();
    depth = Math.max(depth, curDepth);
    if (node.left) stack.push({ node: node.left, depth: curDepth + 1 });
    if (node.right) stack.push({ node: node.right, depth: curDepth + 1 });
  }
  return depth;
};

// 广度优先遍历
var maxDepth = function(root) {
  if (root === null) return 0;
  const queue = [root];
  let depth = 0;
  while (queue.length) {
    let levelSize = queue.length; // 当前层的节点数
    while (levelSize--) {
      const node = queue.shift();
      if (node.left) queue.push(node.left);
      if (node.right) queue.push(node.right);
    }
    depth++;
  }
  return depth;
};

二叉树的最小深度

题目地址 (opens new window)

// 递归
var minDepth = function(root) {
  if (root === null) return 0;

  const left = minDepth(root.left);
  const right = minDepth(root.right);

  if (left > 0 && right > 0) {
    return Math.min(left, right) + 1;
  } else if (left > 0) {
    return left + 1;
  } else if (right > 0) {
    return right + 1;
  } else {
    return 1;
  }
};

// 深度优先遍历
var minDepth = function(root) {
  if (root === null) return 0;
  const queue = [[root, 1]];
  while (queue.length) {
    const [node, depth] = queue.shift();
    if (node.left === null && node.right === null) return depth;
    if (node.left) queue.push([node.left, depth + 1]);
    if (node.right) queue.push([node.right, depth + 1]);
  }
};

// 广度优先遍历
var minDepth = function(root) {
  if (root === null) return 0;
  const queue = [root];
  let depth = 1;
  while (queue.length) {
    let levelSize = queue.length;
    while (levelSize--) {
      const node = queue.shift();
      if (node.left === null && node.right === null) return depth;
      if (node.left) queue.push(node.left);
      if (node.right) queue.push(node.right);
    }
    depth++;
  }
};

二叉树的层序遍历

题目地址 (opens new window)

// 广度优先遍历
var levelOrder = function(root) {
  if (root === null) return [];
  const queue = [root];
  const res = [];
  while (queue.length) {
    const temp = [];
    let levelSize = queue.length;
    while (levelSize--) {
      const node = queue.shift();
      temp.push(node.val);
      if (node.left) queue.push(node.left);
      if (node.right) queue.push(node.right);
    }
    res.push(temp);
  }
  return res;
};

路径总和

题目地址 (opens new window)

// 递归
var hasPathSum = function(root, targetSum) {
  if (root === null) return false;
  if (root.left === null && root.right === null) return targetSum === root.val;
  return (
    hasPathSum(root.left, targetSum - root.val) ||
    hasPathSum(root.right, targetSum - root.val)
  );
};

// 深度优先遍历
var hasPathSum = function(root, targetSum) {
  if (root === null) return false;
  const stack = [root];
  while (stack.length) {
    const node = stack.pop();
    if (node.left === null && node.right === null) {
      if (node.val === targetSum) return true;
    }
    if (node.left) {
      node.left.val += node.val;
      stack.push(node.left);
    }
    if (node.right) {
      node.right.val += node.val;
      stack.push(node.right);
    }
  }
  return false;
};

// 广度优先遍历
var hasPathSum = function(root, targetSum) {
  if (root === null) return false;
  const queue = [root];
  while (queue.length) {
    let levelSize = queue.length;
    while (levelSize--) {
      const node = queue.shift();
      if (node.left === null && node.right === null) {
        if (node.val === targetSum) return true;
      }
      if (node.left) {
        node.left.val += node.val;
        queue.push(node.left);
      }
      if (node.right) {
        node.right.val += node.val;
        queue.push(node.right);
      }
    }
  }
  return false;
};

翻转二叉树

题目地址 (opens new window)

var invertTree = function(root) {
  if (root === null) return root;
  const left = invertTree(root.left);
  const right = invertTree(root.right);
  root.left = right;
  root.right = left;
  return root;
};

相同的树

题目地址 (opens new window)

var isSameTree = function(p, q) {
  if (p === null && q === null) return true;
  if (p === null || q === null || p.val !== q.val) return false;
  return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
};

对称二叉树

题目地址 (opens new window)

var isSymmetric = function(root) {
  function symmetryTree(l, r) {
    if (l === null && r === null) return true;
    if (l === null || r === null) return false;
    return (
      l.val === r.val &&
      symmetryTree(l.left, r.right) &&
      symmetryTree(l.right, r.left)
    );
  }

  return symmetryTree(root, root);
};

平衡二叉树

题目地址 (opens new window)

var isBalanced = function(root) {
  return checkTree(root) !== -1;
};

function checkTree(root) {
  if (root === null) return 0;
  const left = checkTree(root.left);
  if (left === -1) return -1;
  const right = checkTree(root.right);
  if (right === -1) return -1;
  return Math.abs(left - right) < 2 ? Math.max(left, right) + 1 : -1;
}

验证二叉搜索树

题目地址 (opens new window)

方法一：中序遍历

二叉搜索树中序遍历得到的序列一定是升序的。

var isValidBST = function(root) {
  let stack = [];
  let inorder = -Infinity;

  while (stack.length || root !== null) {
    while (root !== null) {
      stack.push(root);
      root = root.left;
    }
    root = stack.pop();
    if (root.val <= inorder) {
      // 如果当前节点的值小于等于前一个中序遍历到的节点的值，说明不是二叉搜索树
      return false;
    }
    inorder = root.val;
    root = root.right;
  }
  return true;
};

方法二：递归

var isValidBST = function(root) {
  return check(root, -Infinity, Infinity);
};
function check(root, leftVal, rightVal) {
  if (root === null) return true;
  if (root.val <= leftVal || root.val >= rightVal) return false;
  return (
    check(root.left, leftVal, root.val) && check(root.right, root.val, rightVal)
  );
}

二叉树的最近公共祖先

题目地址 (opens new window)

var lowestCommonAncestor = function(root, p, q) {
  if (root === null || p === root || q === root) return root;
  let left = lowestCommonAncestor(root.left, p, q);
  let right = lowestCommonAncestor(root.right, p, q);
  if (left === null) return right;
  if (right === null) return left;
  return root;
};

二叉搜索树的最近公共祖先

题目地址 (opens new window)

var lowestCommonAncestor = function(root, p, q) {
  if (root === null) return root;
  if (p.val < root.val && q.val < root.val) {
    return lowestCommonAncestor(root.left, p, q);
  }
  if (p.val > root.val && q.val > root.val) {
    return lowestCommonAncestor(root.right, p, q);
  }
  return root;
};

var lowestCommonAncestor = function(root, p, q) {
  while (root) {
    if (p.val < root.val && q.val < root.val) {
      root = root.left;
    } else if (p.val > root.val && q.val > root.val) {
      root = root.right;
    } else {
      break;
    }
  }
  return root;
};

二叉树最大宽度

题目地址 (opens new window)

var widthOfBinaryTree = function(root) {
  const queue = [[root, 1n]];
  let res = -1;
  while (queue.length) {
    let levelSize = queue.length;
    res = Math.max(res, Number(queue[queue.length - 1][1] - queue[0][1] + 1n));
    while (levelSize--) {
      const [node, index] = queue.shift();
      if (node.left) queue.push([node.left, index * 2n]);
      if (node.right) queue.push([node.right, index * 2n + 1n]);
    }
  }
  return res;
};

图

图的概念和用途

• 图由边的集合和顶点的集合组成。比如每一个城市就是一个顶点，每一条道路就是一条边。

• 图的常见应用包括社交网络分析、网络拓扑、路径搜索、推荐系统、路由算法等。

• 顶点也有权重，也称为成本。如果一个图的顶点对是有序的，则称之为有向图。在对有向图中的顶点排序后，便可以在两个顶点之间绘制一个箭头。有向图表明了顶点的流向。流程图就是有向图的一个例子。

• 如果图是无序的，则称之为无序图或无向图。

• 从一个顶点走到另一个顶点的这组边称为路径。路径中所有的顶点都由边连接。路径的长度用路径中第一个顶点到最后一个顶点之间的边的数量表示。指向自身顶点组成的路径称为环，环的长度为 0。

• 圈是至少有一条边的路径，且路径的第一个顶点和最后一个顶点相同。无论是有向图还是无向图，只要没有重复顶点的圈就是一个简单圈，除了第一个和最后一个顶点以外，路径的其他顶点有重复的圈称为平凡圈。

• 如果两个顶点之间有路径，那么这两个顶点之间就是强连通的。如果有向图的所有顶点都是强连通的，那么这个有向图也是强连通的。

• 图和邻接表

邻接表适合表示稀疏图，即顶点较少但是边数量较多的图。

• 图和邻接矩阵

邻接表适合表示稠密图，即顶点较多且边数量也较多的图。

• 图遍历

图的代码实现

function Graph(v) {
  this.vertices = v; // 顶点
  this.edges = 0; // 边的数量
  this.adj = []; // 邻接表
  this.marked = []; // 存储顶点的状态，是否被访问过
  // 创建二维数组，邻接表是一个二维数组
  for (var i = 0; i < this.vertices; i++) {
    this.adj[i] = [];
    this.marked[i] = false;
  }
  this.shortestPath = []; // 用一个数组来记录最短路径所有的边
  this.hasPath = hasPath; // 判断是否有路径
  this.findShortestPath = findShortestPath; // 寻找最短路径
  this.addEdge = addEdge; // 添加边
  this.showGraph = showGraph; // 打印图
  this.dfs = dfs; // 深度优先搜索
  this.bfs = bfs; // 广度优先搜索
}

// 添加边，参数是两个顶点
function addEdge(v, w) {
  this.adj[v].push(w);
  this.adj[w].push(v);
  this.edges++;
}

// 打印图，其实就是打印邻接表
function showGraph() {
  for (var i = 0; i < this.vertices; i++) {
    var edges = "";
    for (var j = 0; j < this.vertices; j++) {
      // 判断两个顶点之间是否有边
      if (this.adj[i][j]) {
        edges += this.adj[i][j] + " ";
      }
    }
    console.log(i + "->" + edges);
  }
}

// 深度优先搜索
function dfs(v) {
  // 标记初始顶点已经被访问过
  this.marked[v] = true;
  // 如果该顶点在邻接表中有值，说明图中有与之相连的边，可以打印该顶点
  if (this.adj[v]) {
    console.log("深度优先搜索结果：顶点 " + v + " 已经被访问过了！");
  }
  // 遍历跟该顶点项相连的其他顶点
  for (var w in this.adj[v]) {
    var current = this.adj[v][w];
    // 如果当前顶点没被访问过
    if (!this.marked[current]) {
      // 递归遍历
      this.dfs(current);
    }
  }
}

// 广度优先搜索
function bfs(v) {
  var queue = []; // 队列
  this.marked[v] = true; // 标记初始顶点已经被访问过
  queue.push(v); // 将访问过的顶点放入队列中
  while (queue.length > 0) {
    var q = queue.shift(); // 逐个出列，并寻找与出列顶点相连的其他顶点
    if (q !== undefined) {
      console.log("广度优先搜索结果：顶点 " + q + " 已经被访问过了！");
    }
    // 遍历与出列顶点相连的其他顶点
    for (var w in this.adj[q]) {
      var current = this.adj[q][w];
      // 如果当前节点没被访问过
      if (!this.marked[current]) {
        this.marked[current] = true; // 标记为以访问
        this.shortestPath[current] = q; // 说明有一条边可以从 current 顶点到 q 顶点
        queue.push(current); // 并将该顶点放入队列中
      }
    }
  }
}

// 判断是否有路径
function hasPath(v) {
  // 如果当前顶点有被访问，说明就有路径
  return this.marked[v];
}

// 寻找最短路径，它的实现是基于广度优先搜索的
function findShortestPath(v) {
  var source = 0;
  if (!this.hasPath(v)) {
    return undefined;
  }
  var path = [];
  for (var i = v; i !== source; i = this.shortestPath[i]) {
    path.push(i);
  }
  path.push(source);
  return path;
}

var graph = new Graph(5);
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(1, 3);
graph.addEdge(2, 4);
graph.showGraph();
// graph.dfs(0);
graph.bfs(0);
var paths = graph.findShortestPath(4); // 寻找从顶点 0 到顶点 4 的最短路径
// 方便展示最短路径
var str = "";
while (paths.length) {
  if (paths.length > 1) {
    str += paths.pop() + "->";
  } else {
    str += paths.pop();
  }
}
console.log(str);

图的另一种实现

var Queue = function() {
  var items = [];
  //入队
  this.enqueue = function(element) {
    items.push(element);
  };
  // 出队
  this.dequeue = function() {
    return items.shift();
  };
  //查看队列头
  this.front = function() {
    return items[0];
  };
  //检查队列是否为空
  this.isEmpty = function() {
    return items.length === 0;
  };
  //队列大小
  this.size = function() {
    return items.length;
  };
};
/*
 * 图
 * 1、可用于实现地图、社交网络等
 * 2、有向图和无向图
 * 3、表示图结构的方式：邻接矩阵、邻接表
 * 4、图遍历：广度优先和深度优先
 * 5、每个节点有三种状态：未发现、已发现、已探索
 */
var Graph = function() {
  var vertices = []; // 图的顶点，以数组形式存储每个顶点
  var edges = {}; // 图的边，以对象形式存储每个顶点包含的边

  // 添加顶点
  this.addVertex = function(v) {
    vertices.push(v);
    edges[v] = [];
  };

  // 添加边
  this.addEdge = function(a, b) {
    edges[a].push(b);
    edges[b].push(a);
    console.log(edges);
  };

  // 打印图的邻接表
  this.print = function() {
    var str = "";
    for (var i = 0; i < vertices.length; i++) {
      var vertice = vertices[i];
      str += vertice + " => ";
      var edge = edges[vertice];
      for (var j = 0; j < edge.length; j++) {
        str += edge[j] + " ";
      }
      str += "\n";
    }
    console.log(str);
  };

  // 广度优先遍历，white为未发现，grey为已发现，black为已探索
  var initColor = function() {
    // 将所有顶点的颜色置为白色，表示未发现
    var color = {};
    for (var i = 0; i < vertices.length; i++) {
      color[vertices[i]] = "white";
    }
    return color;
  };
  this.bfs = function(v, callback) {
    var color = initColor();
    var queue = new Queue();
    queue.enqueue(v);
    while (!queue.isEmpty()) {
      var currVertice = queue.dequeue(); // 顶点出列
      var currEdge = edges[currVertice]; // 存储该顶点相关的边
      for (var i = 0; i < currEdge.length; i++) {
        // 遍历该顶点相关的所有边
        var nextVertice = currEdge[i]; // 与该顶点相连的其他所有顶点
        if (color[nextVertice] == "white") {
          // 未发现的顶点全部入列，并标识为已发现
          queue.enqueue(nextVertice);
          color[nextVertice] = "grey";
        }
      }
      color[currVertice] = "black"; // 遍历结束后将该顶点标识为已探索
      if (callback) {
        // 回调函数
        callback(currVertice);
      }
    }
  };

  // 带最短路径的广度优先算法
  this.BFS = function(v, callback) {
    var color = initColor();
    var queue = new Queue();
    var distance = {}; // 存储某个顶点到其它顶点的距离
    var backPoint = {}; // 存储某个顶点的回溯点
    for (var i = 0; i < vertices.length; i++) {
      distance[vertices[i]] = 0;
      backPoint[vertices[i]] = null;
    }
    queue.enqueue(v);
    while (!queue.isEmpty()) {
      var currVertice = queue.dequeue(); // 顶点出列
      var currEdge = edges[currVertice]; // 存储该顶点相关的边
      for (var i = 0; i < currEdge.length; i++) {
        // 遍历该顶点相关的所有边
        var nextVertice = currEdge[i]; // 与该顶点相连的其他所有顶点
        if (color[nextVertice] == "white") {
          // 未发现的顶点全部入列，并标识为已发现
          queue.enqueue(nextVertice);
          color[nextVertice] = "grey";
          backPoint[nextVertice] = currVertice; // 设置回溯点
          distance[nextVertice] = distance[currVertice] + 1; // 设置距离
        }
      }
      color[currVertice] = "black"; // 遍历结束后将该顶点标识为已探索
      if (callback) {
        // 回调函数
        callback(currVertice);
      }
    }
    return {
      backPoint: backPoint,
      distance: distance
    };
  };

  // 深度优先算法
  var dfs = function(u, color, callback) {
    color[u] = "grey";
    var n = edges[u];
    for (var i = 0; i < n.length; i++) {
      var w = n[i];
      if (color[w] == "white") {
        dfs(w, color, callback);
      }
    }
    color[u] = "black";
    if (callback) {
      callback(u);
    }
  };
  this.DFS = function(v, callback) {
    var color = initColor();
    dfs(v, color, callback);
  };
};
var g = new Graph();
g.addVertex("A");
g.addVertex("B");
g.addVertex("C");
g.addVertex("D");
g.addVertex("E");
g.addVertex("F");
g.addEdge("A", "B");
g.addEdge("A", "C");
g.addEdge("A", "D");
g.addEdge("C", "D");
g.addEdge("B", "E");
g.addEdge("F", "B");
g.print();

var Stack = function() {
  var items = []; //私有

  // push 栈顶添加元素
  this.push = function(element) {
    items.push(element);
  };
  // pop 移除栈顶元素
  this.pop = function() {
    return items.pop();
  };
  // peek 检查栈顶
  this.peek = function() {
    return items[items.length - 1];
  };

  // 检查栈 是否为空
  this.isEmpty = function() {
    return items.length == 0;
  };

  // 清除栈
  this.clear = function() {
    items = [];
  };

  // 获取栈的大小
  this.size = function() {
    return items.length;
  };

  // 检查items
  this.getItems = function() {
    return items;
  };
};

// 实现最短路径算法：从当前点出发，寻找回溯点。广度优先算法保证了每个顶点的回溯点是最近的。
var paths = g.BFS("A");
var ShortestPath = function(from, to) {
  var currVertice = to;
  var path = new Stack();
  while (currVertice != from) {
    path.push(currVertice);
    currVertice = paths.backPoint[currVertice];
  }
  path.push(currVertice);
  var str = "";
  while (!path.isEmpty()) {
    str += path.pop() + "-";
  }
  str = str.slice(0, str.length - 1);
  console.log(from + "到" + to + "的最短路径为：" + str);
};
ShortestPath("A", "F");

图的深度优先遍历

// 使用记忆化优化，时间复杂度是：O(V+E)，空间复杂度是：O(V)
const graph = {
  A: ["B", "C"],
  B: ["D", "E"],
  C: ["F"],
  D: [],
  E: [],
  F: []
};

const dfsMemorization = (graph, start) => {
  const visited = new Set();

  const dfs = (node) => {
    if (visited.has(node)) return;
    visited.add(node);
    console.log(node);

    for (const neighbor of graph[node]) {
      dfs(neighbor);
    }
  };

  dfs(start);
};

dfsMemorization(graph, "A"); // A B D E C F

图的广度优先遍历

// 使用记忆化+优先级队列优化，时间复杂度是：O(V+E)，空间复杂度是：O(V)
const graph = {
  A: ["B", "C"],
  B: ["D", "E"],
  C: ["F"],
  D: [],
  E: [],
  F: []
};

const bfsPriorityQueue = (graph, start) => {
  const visited = new Set();
  const queue = [];
  queue.push(start);

  while (queue.length) {
    const node = queue.shift();
    if (visited.has(node)) continue;
    visited.add(node);
    console.log(node);

    // 根据一些优先级规则对相邻节点进行排序，例如按字母顺序或节点值的大小等
    const neighbors = graph[node].sort();

    for (const neighbor of neighbors) {
      queue.push(neighbor);
    }
  }
};

bfsPriorityQueue(graph, "A"); // A B C D E F

克隆图

题目地址 (opens new window)

var cloneGraph = function(node) {
  if (node === null) return null;

  const visited = new Map();
  const stack = [node];
  const clone = new Node(node.val, []);

  visited.set(node, clone);

  while (stack.length) {
    const cur = stack.pop();
    const cloneCur = visited.get(cur);

    for (const neighbor of cur.neighbors) {
      if (!visited.has(neighbor)) {
        const cloneNeigbor = new Node(neighbor.val, []);
        visited.set(neighbor, cloneNeigbor);
        stack.push(neighbor);
      }
      cloneCur.neighbors.push(visited.get(neighbor));
    }
  }

  return clone;
};

堆

从图中可以看出，斐波那契堆和严格斐波那契堆的效率是最好的。

二叉堆的定义和特性

1. 二叉堆是计算机科学中一种非常著名的数据结构，由于它能高效、快速地找出最大值和最小值，常被应用于优先队列。它也被用于著名的堆排序算法中。

2. 二叉堆是一种特殊的二叉树，有以下两个特性。

• 它是一棵完全二叉树，表示树的每一层都有左侧和右侧子节点（除了最后一层的叶节点）， 并且最后一层的叶节点尽可能都是左侧子节点，这叫作结构特性。

• 二叉堆分为最小堆和最大堆。最小堆中任何一个节点的值，都小于或等于它左、右孩子节点的值。最大堆中任何一个节点的值，都大于或等于它左、右孩子节点的值。

• 二叉堆的根节点叫作堆顶。最大堆的堆顶是整个堆中的最大元素；最小堆的堆顶是整个堆中的最小元素。

3. 尽管二叉堆是二叉树，但并不一定是二叉搜索树（BST）。在二叉堆中，每个子节点都要大于等于父节点（最小堆）或小于等于父节点（最大堆）。然而在二叉搜索树中，左侧子节点总是比父节点小，右侧子节点也总是更大。

4. 对于堆中的第 n 个元素：

• 它的左子节点为 2 * n + 1；

• 它的右子节点为 2 * n + 2；

• 它的父节点为 (n - 1) / 2；

• 最后一个非叶子节点为 Math.floor(arr.length / 2) - 1。

5. JS 中常用数组表示堆。

二叉堆的自我调整

1. 所谓堆的自我调整，就是把一个不符合堆性质的完全二叉树，调整成一个堆。

2. 对于二叉堆，有如下几种操作。

• 插入节点。

• 删除节点。

• 构建二叉堆。

这几种操作都基于堆的自我调整。下面以最小堆为例，看一看二叉堆是如何进行自我调整的。

插入节点

当二叉堆插入节点时，插入位置是完全二叉树的最后一个位置。例如插入一个新节点，值是 0。

这时，新节点的父节点 5 比 0 大，显然不符合最小堆的性质。于是让新节点 “上浮”，和父节点交换位置。

继续用节点 0 和父节点 3 做比较，因为 0 小于 3，则让新节点继续 “上浮”

继续比较，最终新节点 0 “上浮” 到了堆顶位置。

删除节点

二叉堆删除节点的过程和插入节点的过程正好相反，所删除的是处于堆顶的节点。例如删除最小堆的堆顶节点 1。

这时，为了继续维持完全二叉树的结构，我们把堆的最后一个节点 10 临时补到原本堆顶的位置。

接下来，让暂处堆顶位置的节点 10 和它的左、右孩子进行比较，如果左、右孩子节点中最小的一个（显然是节点 2）比节点 10 小，那么让节点 10 “下沉”。

继续让节点 10 和它的左、右孩子做比较，左、右孩子中最小的是节点 7，由于 10 大于 7，让节点 10 继续 “下沉”。

这样一来，二叉堆重新得到了调整。

构建二叉堆

构建二叉堆，也就是把一个无序的完全二叉树调整为二叉堆，本质就是让所有非叶子节点依次 “下沉”。

下面举一个无序完全二叉树的例子，如下图所示。

首先，从最后一个非叶子节点开始，也就是从节点 10 开始。如果节点 10 大于它左、右孩子节点中最小的一个，则节点 10 “下沉”。

接下来轮到节点 3，如果节点 3 大于它左、右孩子节点中最小的一个，则节点 3 “下沉”。

然后轮到节点 1，如果节点 1 大于它左、右孩子节点中最小的一个，则节点 1 “下沉”。事实上节点 1 小于它的左、右孩子，所以不用改变。

接下来轮到节点 7，如果节点 7 大于它左、右孩子节点中最小的一个，则节点 7 “下沉”。

节点 7 继续比较，继续 “下沉”。

经过上述几轮比较和 “下沉” 操作，最终每一节点都小于它的左、右孩子节点，一个无序的完全二叉树就被构建成了一个最小堆。

二叉堆的时间复杂度

堆的插入操作是单一节点的 “上浮”，堆的删除操作是单一节点的 “下沉”，这两个操作的平均交换次数都是堆高度的一半，所以时间复杂度是 O(logn)。构建堆的时间复杂度是 O(n)。因此堆排序的时间复杂度是 O(nlogn)。

二叉堆的实现

二叉堆虽然是一个完全二叉树，但它的存储方式并不是链式存储，而是顺序存储。换句话说，二叉堆的所有节点都存储在数组中。

在数组中，在没有左、右指针的情况下，如何定位一个父节点的左孩子和右孩子呢?

像上图那样，可以依靠数组下标来计算。

假设父节点的下标是 parent，那么它的左孩子下标就是 2×parent+1；右孩子下标就是 2×parent+2。

下面实现的是最小堆。

/*
 * “上浮” 操作
 * @param array 待调整的堆
 */
function upAdjust(array) {
  let childIndex = array.length - 1;
  let parentIndex = Math.floor((childIndex - 1) / 2);
  // temp 保存插入的叶子节点值，用于最后赋值
  const temp = array[childIndex];
  while (childIndex > 0 && temp < array[parentIndex]) {
    // 无须真正交换，单向赋值即可
    array[childIndex] = array[parentIndex];
    childIndex = parentIndex;
    parentIndex = Math.floor((parentIndex - 1) / 2);
  }
  array[childIndex] = temp;
}

/*
 * “下沉” 操作
 * @param array 待调整的堆
 * @param parentIndex 要 “下沉” 的父节点
 * @param length 堆的有效大小
 */
function downAdjust(array, parentIndex, length) {
  // temp 保存父节点值，用于最后的赋值
  const temp = array[parentIndex];
  let childIndex = 2 * parentIndex + 1;
  while (childIndex < length) {
    // 如果有右孩子，且右孩子小于左孩子的值，则定位到右孩子
    if (childIndex + 1 < length && array[childIndex + 1] < array[childIndex]) {
      childIndex++;
    }
    // 如果父节点小于任何一个孩子的值，则直接跳出
    if (temp <= array[childIndex]) break;
    // 无须真正交换，单向赋值即可
    array[parentIndex] = array[childIndex];
    parentIndex = childIndex;
    childIndex = 2 * childIndex + 1;
  }
  array[parentIndex] = temp;
}

/*
 * 构建堆
 * @param array 待调整的堆
 */
function buildHeap(array) {
  // 从最后一个非叶子节点开始，依次做 “下沉” 调整
  for (let i = Math.floor((array.length - 2) / 2); i >= 0; i--) {
    downAdjust(array, i, array.length);
  }
}

const arr = [1, 3, 2, 6, 5, 7, 8, 9, 10, 0];
upAdjust(arr);
console.log(arr); // [0, 1, 2, 6, 3, 7, 8, 9, 10, 5]
const arr1 = [7, 1, 3, 10, 5, 2, 8, 9, 6];
buildHeap(arr1);
console.log(arr1); // [1, 5, 2, 6, 7, 3, 8, 9, 10]

上述代码中有一个优化的点，就是在父节点和孩子节点做连续交换时，并不一定要真的交换，只需要先把交换一方的值存入 temp 变量，做单向覆盖，循环结束后，再把 temp 的值存入交换后的最终位置即可。

使用最大堆实现从小到大排序

1. 把无序数组构建成二叉堆。

• 升序：一般采用最大堆；

• 降序：一般采用最小堆。

2. 循环删除堆顶元素，替换到二叉堆的末尾，调整堆产生新的堆顶。

/*
 * “下沉” 操作
 * @param array 待调整的堆
 * @param parentIndex 要 “下沉” 的父节点
 * @param length 堆的有效大小
 */
function downAdjust(array, parentIndex, length) {
  // temp 保存父节点值，用于最后的赋值
  const temp = array[parentIndex];
  let childIndex = 2 * parentIndex + 1;
  while (childIndex < length) {
    // 如果有右孩子，且右孩子大于左孩子的值，则定位到右孩子
    if (childIndex + 1 < length && array[childIndex + 1] > array[childIndex]) {
      childIndex++;
    }
    // 如果父节点大于任何一个孩子的值，则直接跳出
    if (temp >= array[childIndex]) break;
    // 无须真正交换，单向赋值即可
    array[parentIndex] = array[childIndex];
    parentIndex = childIndex;
    childIndex = 2 * childIndex + 1;
  }
  array[parentIndex] = temp;
}

/*
 * 堆排序（升序）
 * @param array 待调整的堆
 */
function heapSort(array) {
  // 1. 把无序数组构建成最大堆
  for (let i = Math.floor((array.length - 2) / 2); i >= 0; i--) {
    downAdjust(array, i, array.length);
  }
  // 2. 循环删除堆顶元素，移到集合尾部，调整堆产生新的堆顶
  for (let i = array.length - 1; i > 0; i--) {
    // 最后 1 个元素和第 1 个元素进行交换
    const temp = array[i];
    array[i] = array[0];
    array[0] = temp;
    // “下沉” 调整最大堆
    downAdjust(array, 0, i);
  }
}

const arr = [3, 2, 3, 1, 2, 4, 5, 5, 6];
heapSort(arr);
console.log(arr); // [1, 2, 2, 3, 3, 4, 5, 5, 6]

数组中的第 K 个最大元素

题目地址 (opens new window)

var findKthLargest = function(nums, k) {
  nums.sort((a, b) => b - a);
  return nums[k - 1];
};

var findKthLargest = function(nums, k) {
  nums.sort((a, b) => a - b);
  return nums[nums.length - k];
};

/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number}
 */
var findKthLargest = function(nums, k) {
  let heapSize = nums.length; // 堆大小

  const swap = (a, i, j) => {
    let temp = a[i];
    a[i] = a[j];
    a[j] = temp;
  };

  // 从左向右，从上到下调整节点
  const maxHeapify = (nums, i, heapSize) => {
    const l = 2 * i + 1; // 左子节点
    const r = 2 * i + 2; // 右子节点
    let largest = i;
    if (l < heapSize && nums[l] > nums[largest]) {
      largest = l;
    }
    if (r < heapSize && nums[r] > nums[largest]) {
      largest = r;
    }
    if (largest !== i) {
      swap(nums, i, largest); // 找到左右子节点中较大的元素交换
      maxHeapify(nums, largest, heapSize); // 递归交换后面的节点
    }
  };

  const buildMaxHeap = (nums, heapSize) => {
    for (let i = Math.floor(nums.length / 2) - 1; i >= 0; i--) {
      // 从最后一个非叶子节点开始构建堆
      maxHeapify(nums, i, heapSize);
    }
  };

  buildMaxHeap(nums, heapSize); // 构建大顶堆
  // 前 k-1 个堆顶元素不断和数组的末尾元素交换，然后重新调整节点
  for (let i = nums.length - 1; i >= nums.length - k + 1; i--) {
    swap(nums, 0, i); // 交换堆顶和数组末尾元素
    heapSize--; // 堆大小减 1
    maxHeapify(nums, 0, heapSize); // 重新调整节点
  }
  return nums[0]; // 返回堆顶元素，就是第 k 大元素
};

/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number}
 */
var findKthLargest = function(nums, k) {
  let heapSize = nums.length;

  // 下沉操作
  const downAdjust = (array, parentIndex, length) => {
    // temp 保存父节点值，用于最后的赋值
    const temp = array[parentIndex];
    let childIndex = 2 * parentIndex + 1; // 左孩子
    while (childIndex < length) {
      // 如果有右孩子，且右孩子大于左孩子的值，则定位到右孩子
      if (
        childIndex + 1 < length &&
        array[childIndex + 1] > array[childIndex]
      ) {
        childIndex++;
      }
      // 如果父节点大于任何一个孩子的值，则直接跳出
      if (temp >= array[childIndex]) break;
      // 无须真正交换，单向赋值即可
      array[parentIndex] = array[childIndex];
      parentIndex = childIndex;
      childIndex = 2 * childIndex + 1;
    }
    array[parentIndex] = temp;
  };

  const buildMaxHeap = (nums, heapSize) => {
    for (let i = Math.floor(nums.length / 2) - 1; i >= 0; i--) {
      // 从最后一个非叶子节点开始构建堆
      downAdjust(nums, i, heapSize);
    }
  };

  buildMaxHeap(nums, heapSize); // 构建大顶堆

  // 前 k-1 个堆顶元素不断和数组的末尾元素交换，然后重新调整节点
  for (let i = nums.length - 1; i >= nums.length - k + 1; i--) {
    [nums[0], nums[i]] = [nums[i], nums[0]]; // 交换堆顶和数组末尾元素
    heapSize--; // 堆大小减 1
    downAdjust(nums, 0, heapSize); // 重新调整节点
  }

  return nums[0]; // 返回堆顶元素，就是第 k 大元素
};

前 K 个高频元素

题目地址 (opens new window)

var topKFrequent = function(nums, k) {
  const map = new Map();
  for (const n of nums) {
    map.set(n, map.has(n) ? map.get(n) + 1 : 1);
  }
  return [...map.entries()]
    .sort((a, b) => b[1] - a[1])
    .map((item) => item[0])
    .slice(0, k);
};

优先队列

优先队列的特点

正常入队，按照优先级出队。

优先队列不再遵循先入先出（FIFO）的原则，而是分为两种情况。

• 最大优先队列，无论入队顺序如何，都是当前最大的元素优先出队。

• 最小优先队列，无论入队顺序如何，都是当前最小的元素优先出队。

要实现以上需求，利用线性数据结构并非不能实现，但是时间复杂度较高。

优先队列的实现

优先队列的实现一般有两种机制：堆和二叉搜索树。

回顾一下二叉堆的特性。

• 最大堆的堆顶是整个堆中的最大元素。

• 最小堆的堆顶是整个堆中的最小元素。

因此，可以用最大堆来实现最大优先队列，这样的话，每一次入队操作就是堆的插入操作，每一次出队操作就是删除堆顶节点。

优先队列的时间复杂度

由于二叉堆节点 “上浮” 和 “下沉” 的时间复杂度都是 O(logn)，所以优先队列入队和出队的时间复杂度也是 O(logn)。

// 用最大堆来实现最大优先队列
function PriorityQueue() {
  this.array = []; // 存储队列元素
  this.enqueue = enqueue; // 入队
  this.dequeue = dequeue; // 出队
  this.upAdjust = upAdjust; // 堆“上浮”操作
  this.downAdjust = downAdjust; // 堆“下沉”操作
}

/*
 * 入队
 * @param key 入队元素
 */
function enqueue(key) {
  this.array.push(key);
  this.upAdjust();
}

/*
 * 出队
 */
function dequeue() {
  // 获取堆顶元素
  const head = this.array[0];
  // 让最后一个元素移动到堆顶
  this.array[0] = this.array[this.array.length - 1];
  this.downAdjust();
  return head;
}

/*
 * “上浮”调整
 */
function upAdjust() {
  let childIndex = this.array.length - 1;
  let parentIndex = Math.floor((childIndex - 1) / 2);
  // temp 保存插入的叶子节点值，用于最后的赋值
  const temp = this.array[childIndex];
  while (childIndex > 0 && temp > this.array[parentIndex]) {
    // 无须真正交换，单向赋值即可
    this.array[childIndex] = this.array[parentIndex];
    childIndex = parentIndex;
    parentIndex = Math.floor(parentIndex / 2);
  }
  this.array[childIndex] = temp;
}

/*
 * “下沉”调整
 */
function downAdjust() {
  // temp 保存父节点的值，用于最后的赋值
  let parentIndex = 0;
  const temp = this.array[parentIndex];
  let childIndex = 1;

  while (childIndex < this.array.length - 1) {
    // 如果有右孩子，且右孩子大于左孩子的值，则定位到右孩子
    if (
      childIndex + 1 < this.array.length - 1 &&
      this.array[childIndex + 1] > this.array[childIndex]
    ) {
      childIndex++;
    }
    // 如果父节点大于任何一个孩子的值，直接跳出
    if (temp >= this.array[childIndex]) break;
    // 无须真正交换，单向赋值即可
    this.array[parentIndex] = this.array[childIndex];
    parentIndex = childIndex;
    childIndex = 2 * childIndex + 1;
  }
  this.array[parentIndex] = temp;
}

const priorityQueue = new PriorityQueue();
priorityQueue.enqueue(3);
priorityQueue.enqueue(5);
priorityQueue.enqueue(10);
priorityQueue.enqueue(2);
priorityQueue.enqueue(7);
console.log(priorityQueue.array);
console.log("出队元素：" + priorityQueue.dequeue()); // 出队元素：10
console.log("出队元素：" + priorityQueue.dequeue()); // 出队元素：7

数据流中的第 K 大元素

题目地址 (opens new window)

方法一：将现有数据流中的元素从大到小进行排序，每次取到的第 K 个元素就是数据流中的第 K 大元素。这种方法的时间复杂度为：O(nlogn)。

方法二：可以维护一个最小堆（最小优先队列），并且堆的大小等于 K，每次有新的数据进来时，都跟堆顶元素进行比较。如果小于堆顶元素，就不用管；如果大于堆顶元素，就将现有的堆顶元素干掉，新数据加进堆中，并调整堆中元素的顺序，保证堆顶元素永远是最小的。这种方法初始化的时间复杂度为：O(nlogk) ，单次插入的时间复杂度为：O(logk)，相比方法一效率提高很多。

滑动窗口最大值

题目地址 (opens new window)

方法一：维护一个最大堆（最大优先队列）。时间复杂度为：O(nlogn)。

方法二：使用具有单调性的双端队列（单调队列）。时间复杂度为：O(n)。

var maxSlidingWindow = function(nums, k) {
  const n = nums.length;
  const queue = []; // 存放单调队列的下标，对应 nums 中的元素是严格单调递减的
  for (let i = 0; i < k; i++) {
    // 新加入的元素大于等于队尾元素时，就可以弹出队尾元素，直到新加入元素小于队尾元素或者队列为空。这样就能保证队首元素对应的 nums 中的值是最大的
    while (queue.length && nums[i] >= nums[queue[queue.length - 1]]) {
      queue.pop();
    }
    queue.push(i);
  }
  const res = [nums[queue[0]]];
  for (let i = k; i < n; i++) {
    while (queue.length && nums[i] >= nums[queue[queue.length - 1]]) {
      queue.pop();
    }
    queue.push(i);
    // 如果队首元素不在滑动窗口中，也应该去掉
    while (queue[0] <= i - k) {
      queue.shift();
    }
    res.push(nums[queue[0]]);
  }
  return res;
};

字典树

字典树的概念和用途

字典树（Trie 树），又称单词查找树或者键树，是一种树形结构，是一种哈希树的变种。
典型应用是用于统计和排序大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。
它的优点是：最大限度地减少无谓的字符串比较，查询效率比哈希表高。
Trie 的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。

图中的数字代表单词出现的频次。

字典树的基本性质

• 根节点不包含字符，除根节点外每一个节点都只包含一个字符。

• 从根节点到某一个节点，路径上经过的字符连接起来，就是该节点对应的字符串。

• 每个节点的所有子节点包含的字符都不相同。

实现 Trie (前缀树)

题目地址 (opens new window)

var TrieNode = function() {
  this.children = {};
  this.isEnd = false;
};

var Trie = function() {
  this.root = new TrieNode();
};

// 插入
Trie.prototype.insert = function(word) {
  if (!word) return;
  let node = this.root;
  for (const c of word) {
    if (!node.children[c]) {
      node.children[c] = new TrieNode();
    }
    node = node.children[c];
  }
  node.isEnd = true;
};

// 查询
Trie.prototype.search = function(word) {
  if (!word) return false;
  let node = this.root;
  for (const c of word) {
    if (!node.children[c]) {
      return false;
    }
    node = node.children[c];
  }
  return node.isEnd;
};

// 前缀
Trie.prototype.startsWith = function(prefix) {
  if (!prefix) return true;
  let node = this.root;
  for (const c of prefix) {
    if (!node.children[c]) {
      return false;
    }
    node = node.children[c];
  }
  return true;
};

并查集

并查集（Union-find Data Structure）是一种树型的数据结构。它的特点是由子结点找到父亲结点，用于处理一些不交集（Disjoint Sets）的合并及查询问题。

• Find：确定元素属于哪一个子集。它可以被用来确定两个元素是否属于同一子集。
• Union：将两个子集合并成同一个集合。

岛屿数量

题目地址 (opens new window)

class UnionFind {
  constructor(n) {
    this.count = n; // 集合的数量
    this.parent = new Array(n); // 节点的 parent
    this.rank = new Array(n); // 集合的深度，并查集中将深度称为 rank
    for (let i = 0; i < n; i++) {
      this.parent[i] = i; // 初始时节点的 parent 都指向自己
      this.rank[i] = 1;
    }
  }
  find(i) {
    while (this.parent[i] !== i) {
      // 并查集优化二，路经压缩
      this.parent[i] = this.find(this.parent[i]); // 也可以写成：this.parent[i] = this.parent[this.parent[i]];
      i = this.parent[i];
    }
    return i;
  }
  union(x, y) {
    let rootX = this.find(x);
    let rootY = this.find(y);
    if (rootX === rootY) return;
    // 并查集优化一，将深度较小的集合接在深度较大的集合下，这样整体的集合深度会较小
    if (this.rank[rootX] > this.rank[rootY]) {
      this.parent[rootY] = rootX;
    } else if (this.rank[rootX] < this.rank[rootY]) {
      this.parent[rootX] = rootY;
    } else {
      this.parent[rootY] = rootX;
      this.rank[rootX]++;
    }
    this.count--;
  }
  getCount() {
    return this.count;
  }
}

const numIslands = (grid) => {
  const m = grid.length;
  const n = grid[0].length;
  const dirs = [
    [-1, 0],
    [1, 0],
    [0, -1],
    [0, 1]
  ]; // 上下左右 4 个方向
  const uf = new UnionFind(m * n);
  const dummy = -1;
  for (let i = 0; i < m; i++) {
    for (let j = 0; j < n; j++) {
      if (grid[i][j] === "0") {
        uf.union(i * n + j, dummy);
      } else if (grid[i][j] === "1") {
        dirs.map((d) => {
          const r = i + d[0];
          const c = j + d[1];
          if (r >= 0 && r < m && c >= 0 && c < n && grid[r][c] === "1") {
            uf.union(i * n + j, r * n + c);
          }
        });
      }
    }
  }
  return uf.getCount();
};

排序算法的时间和空间复杂度

参见此处

排序算法的稳定性

• 假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且 r[i]在 r[j]之前，而在排序后的序列中，r[i]仍在 r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。排序算法的稳定性 (opens new window)

• 稳定的排序算法有：冒泡排序、插入排序、归并排序、计数排序、桶排序和基数排序。

• 不稳定的排序算法有：选择排序、快速排序、希尔排序、堆排序。

冒泡排序

冒泡排序的思路

1. 依次比较相邻的两个数，如果第一个比第二个小，不变。如果第一个比第二个大，调换顺序。一轮下来，最后一个是最大的数。

2. 对除了最后一个之外的数重复第一步，直到只剩一个数。

冒泡排序的实现

function swap(arr, i, j) {
  const temp = arr[i];
  arr[i] = arr[j];
  arr[j] = temp;
}

//从前往后冒泡
function bubbleSort(arr) {
  if (arr.length < 2) {
    return arr;
  }
  const len = arr.length;
  for (let i = 0; i < len; i++) {
    for (let j = 0; j < len - 1 - i; j++) {
      if (arr[j] > arr[j + 1]) {
        swap(arr, j, j + 1);
      }
    }
  }
  return arr;
}

// 从后往前冒泡
function bubbleSort(arr) {
  if (arr.length < 2) {
    return arr;
  }
  const len = arr.length;
  for (let i = len; i >= 2; i--) {
    for (let j = 0; j <= i - 1; j++) {
      if (arr[j] > arr[j + 1]) {
        swap(arr, j, j + 1);
      }
    }
  }
  return arr;
}

冒泡排序的优化

📌 优化点一

冒泡有一个最大的问题就是这种算法不管不管你有序还是没序，闭着眼睛把你循环比较了再说。

比如这个例子：[ 9，8，7，6，5 ]，一个有序的数组，根本不需要排序，它仍然是双层循环一个不少的把数据遍历干净，这其实就是做了没必要做的事情，属于浪费资源。

针对这个问题，我们可以设定一个临时遍历来标记该数组是否已经有序。如果在本轮排序中，元素有交换，则说明数列无序；如果没有元素交换，则说明数列已然有序，然后直接跳出大循环。

function bubbleSort(arr) {
  const len = arr.length;
  for (let i = 0; i < len; i++) {
    let isSort = true;
    for (let j = 0; j < len - 1 - i; j++) {
      if (arr[j] > arr[j + 1]) {
        swap(arr, j, j + 1);
        isSort = false;
      }
    }
    if (isSort) {
      break;
    }
  }
}

📌 优化点二

以上只是冒泡排序优化的第一步，我们还可以进一步来提升它的性能。

比如有一个新的数组：

3, 4, 2, 1, 5, 6, 7, 8

这个数组的特点是前半部分的元素（3、4、2、1）无序，后半部分的元素（5、6、7、8）按升序排列，并且后半部分元素中的最小值也大于前半部分元素的最大值。

其实这个数组右面的许多元素已经是有序的了，可是如果按照现在的冒泡排序，每一轮还是白白地比较了许多次。这正是冒泡排序中另一个需要优化的点。

这个问题的关键点在于对数组有序区的界定。

那么，该如何避免这种情况呢？我们可以在每一轮排序后，记录下来最后一次元素交换的位置，该位置即为无序数列的边界，再往后就是有序区了。

function bubbleSort(arr) {
  // 记录最后一次交换的位置
  let lastExchangeIndex = 0;
  // 无序数列的边界，每次比较只需要比到这里为止
  let sortBorder = arr.length - 1;
  for (let i = 0; i < arr.length - 1; i++) {
    // 有序标记，每一轮的初始值都是 true
    let isSort = true;
    for (let j = 0; j < sortBorder; j++) {
      if (arr[j] > arr[j + 1]) {
        swap(arr, j, j + 1);
        // 因为有元素进行交换，所以不是有序的，标记变为 false
        isSort = true;
        // 更新为最后一次交换元素的位置
        lastExchangeIndex = j;
      }
    }
    sortBorder = lastExchangeIndex;
    if (isSort) {
      break;
    }
  }
}

在这一版代码中，sortBorder 就是无序数列的边界。在每一轮排序过程中，处于 sortBorder 之后的元素就不需要再进行比较了，肯定是有序的。

鸡尾酒排序

鸡尾酒排序是基于冒泡排序的一种升级排序算法。

鸡尾酒排序的思路

鸡尾酒排序的元素比较和交换过程是双向的。

下面举一个例子。

由 8 个数字组成一个无序数列{2,3,4,5,6,7,8,1}，希望对其进行从小到大的排序。

如果按照冒泡排序的思想，排序过程如下。

元素 2、3、4、5、6、7、8 已经是有序的了，只有元素 1 的位置不对，却还要进行 7 轮排序。

鸡尾酒排序正是要解决这个问题。

如果按照鸡尾酒排序，详细过程如下。

第 1 轮(和冒泡排序一样，8 和 1 交换)

第 2 轮

此时开始不一样了，我们反过来从右往左比较并进行交换。

第 3 轮(虽然实际上已经有序，但是流程并没有结束)

在鸡尾酒排序的第 3 轮，需要重新从左向右比较并进行交换。

1 和 2 比较，位置不变；2 和 3 比较，位置不变；3 和 4 比较，位置不变......6 和 7 比较，位置不变。

没有元素位置进行交换，证明已经有序，排序结束。

这就是鸡尾酒排序的思路。排序过程就像钟摆一样，第 1 轮从左到右，第 2 轮从右到左，第 3 轮再从左到右......

这样，本来要用 7 轮排序的场景，用 3 轮就解决了。

鸡尾酒排序的实现

function swap(arr, i, j) {
  const temp = arr[i];
  arr[i] = arr[j];
  arr[j] = temp;
}

function cocktailSort(arr) {
  const len = arr.length;
  for (let i = 0; i < len / 2; i++) {
    // 有序标记，每一轮的初始值都是 true
    let isSort = true;
    // 奇数轮，从左向右比较和交换
    for (let j = i; j < len - 1 - i; j++) {
      if (arr[j] > arr[j + 1]) {
        swap(arr, j, j + 1);
        // 有元素交换，所以不是有序的，标记变为 false
        isSort = false;
      }
    }
    if (isSort) {
      break;
    }
    // 在偶数轮之前，将 isSort 重新标记为 true
    isSort = true;
    // 偶数轮，从右向左比较和交换
    for (let j = len - 1 - i; j > i; j--) {
      if (arr[j] < arr[j - 1]) {
        swap(arr, j, j - 1);
        // 因为有元素进行交换，所以不是有序的，标记变为 false
        isSort = false;
      }
    }
    if (isSort) {
      break;
    }
  }
}

这段代码是鸡尾酒排序的原始实现。代码外层的大循环控制着所有排序回合，大循环内包含 2 个小循环，第 1 个小循环从左向右比较并交换元素，第 2 个小循环从右向左比较并交换元素。

鸡尾酒排序的适用场景

• 鸡尾酒排序的优点是能够在特定条件下，减少排序的回合数;而缺点也很明显，就是代码量几乎增加了 1 倍。

• 因此，鸡尾酒排序能发挥出优势的场景，就是大部分元素已经有序的情况。

选择排序

选择排序的思路

1. 首先，找到数组中最小的元素，拎出来，将它和数组的第一个元素交换位置，第二步，在剩下的元素中继续寻找最小的元素，拎出来，和数组的第二个元素交换位置，如此循环，直到整个数组排序完成。

2. 至于选大还是选小，这个都无所谓，你也可以每次选择最大的拎出来排，也可以每次选择最小的拎出来的排，只要你的排序的手段是这种方式，都叫选择排序。

选择排序的实现

function swap(arr, i, j) {
  const temp = arr[i];
  arr[i] = arr[j];
  arr[j] = temp;
}

function selectionSort(arr) {
  if (arr.length < 2) {
    return arr;
  }
  const len = arr.length;
  for (let i = 0; i < len - 1; i++) {
    let min = i;
    for (let j = i + 1; j < len; j++) {
      if (arr[j] < arr[min]) {
        min = j;
      }
    }
    swap(arr, i, min);
  }
  return arr;
}

插入排序

插入排序的思路

1. 插入排序的思想和我们打扑克摸牌的时候一样，从牌堆里一张一张摸起来的牌都是乱序的，我们会把摸起来的牌插入到左手中合适的位置，让左手中的牌时刻保持一个有序的状态。

2. 实现时会把数组分为已排序和未排序两部分，第一个数为已排序，其余为未排序。然后从未排序抽出第一个数，和已排序部分比较，插入到合适的位置。重复此操作直到数组排序完成。

插入排序的实现

function insertionSort(arr) {
  if (arr.length < 2) {
    return arr;
  }
  for (let i = 1; i < arr.length; i++) {
    const value = arr[i]; // 弹出数据
    let j = 0;
    for (j = i - 1; j >= 0 && arr[j] > value; j--) {
      // arr[j] 是前一个数字，value 是当前数字
      arr[j + 1] = arr[j]; // 移动数据
    }
    arr[j + 1] = value; // 插入数据
  }
  return arr;
}

希尔排序

希尔排序的思路

1. 希尔排序这个名字，来源于它的发明者希尔，也称作“缩小增量排序”，是插入排序的一种更高效的改进版本。它通过定义一个间隔序列来表示在排序过程中进行比较的元素间隔。

2. 我们知道，插入排序对于大规模的乱序数组的时候效率是比较慢的，因为它每次只能将数据移动一位，希尔排序为了加快插入的速度，让数据移动的时候可以实现跳跃移动，节省了一部分的时间开支。当区间为 1 的时候，它使用的排序方式就是插入排序。

希尔排序的实现

function shellSort(arr) {
  const len = arr.length;
  let gap = 1;
  while (gap < len) {
    gap = gap * 3 + 1;
  }
  while (gap > 0) {
    for (let i = gap; i < len; i++) {
      const temp = arr[i];
      let j = i - gap;
      // 跨区间排序
      while (j >= 0 && arr[j] > temp) {
        arr[j + gap] = arr[j];
        j -= gap;
      }
      arr[j + gap] = temp;
    }
    gap = Math.floor(gap / 3);
  }
}

可能你会问为什么区间要以 gap = gap*3 + 1 去计算，其实最优的区间计算方法是没有答案的，这是一个长期未解决的问题，不过差不多都会取在二分之一到三分之一附近。

归并排序（合并排序）

归并排序的思路

归并算法的核心思想是分治法，就是将一个数组一刀切两半，递归切，直到切成单个元素，然后重新组装合并，单个元素合并成小数组，两个小数组合并成大数组，直到最终合并完成，排序完毕。

归并排序的实现

// 归并排序
function mergeSort(arr) {
  if (arr.length < 2) {
    return arr;
  }

  const middle = Math.floor(arr.length / 2);
  const leftArr = arr.slice(0, middle);
  const rightArr = arr.slice(middle);

  return merge(mergeSort(leftArr), mergeSort(rightArr));
}

// 合并左右数组
function merge(leftArr, rightArr) {
  const arr = [];
  let l = 0,
    r = 0;

  while (l < leftArr.length && r < rightArr.length) {
    if (leftArr[l] < rightArr[r]) {
      arr.push(leftArr[l]);
      l++;
    } else {
      arr.push(rightArr[r]);
      r++;
    }
  }

  return arr.concat(leftArr.slice(l)).concat(rightArr.slice(r));
}

function mergeSort(arr) {
  if (arr.length < 2) {
    return arr;
  }
  const middle = Math.floor(arr.length / 2);
  const leftArr = arr.slice(0, middle);
  const rightArr = arr.slice(middle);

  return merge(mergeSort(leftArr), mergeSort(rightArr));
}

function merge(leftArr, rightArr) {
  const res = [];

  while (leftArr.length && rightArr.length) {
    if (leftArr[0] < rightArr[0]) {
      res.push(leftArr.shift());
    } else {
      res.push(rightArr.shift());
    }
  }

  while (leftArr.length) {
    res.push(leftArr.shift());
  }

  while (rightArr.length) {
    res.push(rightArr.shift());
  }

  return res;
}

快速排序

快速排序的思路

1. 快速排序的核心思想也是分治法，分而治之。它的实现方式是每次从序列中选出一个基准值（可以随机选取），其他数依次和基准值做比较，比基准值大的放右边，比基准值小的放左边，然后再对左边和右边的两组数分别选出一个基准值，进行同样的比较移动，重复步骤，直到最后都变成单个元素，整个数组就成了有序的序列。

2. 基准元素的选择，以及元素的交换，都是快速排序的核心问题。

3. 基准元素的选择最简单的可以选择数组的第 1 个元素。元素的交换方法有双边循环法和单边循环法两种。

基准元素的选择

最简单的方式是选择数列的第 1 个元素。

这种选择在绝大多数情况下是没有问题的。但是，假如有一个原本逆序的数列，期望排序成顺序数列，那么会出现什么情况呢?

我们会发现，整个数列并没有被分成两半，每一轮都只确定了基准元素的位置。

在这种情况下，数列的第 1 个元素要么是最小值，要么是最大值，根本无法发挥分治法的优势。

在这种极端情况下，快速排序需要进行 n 轮，时间复杂度退化成了 O(n^2)。

那么，该怎么避免这种情况发生呢?

其实很简单，我们可以随机选择一个元素作为基准元素，并且让基准元素和数列首元素交换位置。

这样一来，即使在数列完全逆序的情况下，也可以有效地将数列分成两部分。

当然，即使是随机选择基准元素，也会有极小的几率选到数列的最大值或最小值，同样会影响分治的效果。

所以，虽然快速排序的平均时间复杂度是 O(nlogn)，但最坏情况下的时间复杂度是 O(n^2)。

快速排序的简单实现

// 选择第 1 个元素为基准，但是很容易让时间复杂度变成 O(n^2)
function quickSort(arr) {
  if (arr.length < 2) {
    return arr;
  }
  const pivot = arr[0]; // 基准值
  const left = [],
    right = [];
  for (let i = 1; i < arr.length; i++) {
    if (arr[i] < pivot) {
      left.push(arr[i]);
    } else {
      right.push(arr[i]);
    }
  }
  return quickSort(left).concat(pivot, quickSort(right));
}

// 选择中间元素为基准，理论上都能使时间复杂度是 O(nlogn)
function quickSort(arr) {
  if (arr.length < 2) {
    return arr;
  }

  const pivotIndex = Math.floor(arr.length / 2);
  const pivot = arr.splice(pivotIndex, 1)[0];
  const left = [],
    right = [];

  for (let i = 0; i < arr.length; i++) {
    if (arr[i] < pivot) {
      left.push(arr[i]);
    } else {
      right.push(arr[i]);
    }
  }

  return quickSort(left).concat(pivot, quickSort(right));
}

双边循环法的思路

给出原始数列如下，要求对其从小到大进行排序。

4，7，6，5，3，2，8，1

首先，选定基准元素 pivot，并且设置两个指针 left 和 right，指向数列的最左和最右两个元素。

接下来进行第 1 次循环，从 right 指针开始，让指针所指向的元素和基准元素做比较。如果大于或等于 pivot，则指针向左移动；如果小于 pivot，则 right 指针停止移动，切换到 left 指针。

在当前数列中，1 < 4，所以 right 直接停止移动，换到 left 指针，进行下一步行动。

轮到 left 指针行动，让指针所指向的元素和基准元素做比较。如果小于或等于 pivot，则指针向右移动；如果大于 pivot，则 left 指针停止移动。

由于 left 开始指向的是基准元素，判断肯定相等，所以 left 右移 1 位。

由于 7 > 4，left 指针在元素 7 的位置停下。这时，让 left 和 right 指针所指向的元素进行交换。

接下来，进入第 2 次循环，重新切换到 right 指针，向左移动。right 指针先移动到 8，8>4，继续左移。由于 2<4，停止在 2 的位置。

按照这个思路，后续步骤如图所示。

双边循环法的实现

function quickSort(arr, startIndex, endIndex) {
  // 递归结束条件: startIndex 大于或等于 endIndex 时
  if (startIndex >= endIndex) {
    return;
  }
  // 得到基准元素位置
  const pivotIndex = partition(arr, startIndex, endIndex);
  // 根据基准元素，分成两部分进行递归排序
  quickSort(arr, startIndex, pivotIndex - 1);
  quickSort(arr, pivotIndex + 1, endIndex);
}

/*
 * 分治（双边循环法）
 * @param arr 待交换的数组
 * @param startIndex 起始下标
 * @param endIndex 结束下标
 */
function partition(arr, startIndex, endIndex) {
  // 取第1个位置(也可以选择随机位置)的元素作为基准元素
  const pivot = arr[startIndex];
  let left = startIndex;
  let right = endIndex;

  while (left !== right) {
    // 控制 right 指针比较并左移
    while (left < right && arr[right] > pivot) {
      right--;
    }
    // 控制 left 指针比较并右移
    while (left < right && arr[left] <= pivot) {
      left++;
    }
    // 交换 left 和 right 指针所指向的元素
    if (left < right) {
      const temp = arr[left];
      arr[left] = arr[right];
      arr[right] = temp;
    }
  }

  // pivot 和指针重合点交换
  arr[startIndex] = arr[left];
  arr[left] = pivot;
  return left;
}

单边循环法的思路

给出原始数列如下，要求对其从小到大进行排序。

4，7，6，5，3，2，8，1

开始和双边循环法相似，首先选定基准元素 pivot。同时，设置一个 mark 指针指向数列起始位置，这个 mark 指针代表小于基准元素的区域边界。

接下来，从基准元素的下一个位置开始遍历数组。

如果遍历到的元素大于基准元素，就继续往后遍历。

如果遍历到的元素小于基准元素，则需要做两件事：第一，把 mark 指针右移 1 位，因为小于 pivot 的区域边界增大了 1；第二，让最新遍历到的元素和 mark 指针所在位置的元素交换位置，因为最新遍历的元素归属于小于 pivot 的区域。

首先遍历到元素 7，7>4，所以继续遍历。

接下来遍历到的元素是 3，3<4，所以 mark 指针右移 1 位。

随后，让元素 3 和 mark 指针所在位置的元素交换，因为元素 3 归属于小于 pivot 的区域。

按照这个思路，继续遍历，后续步骤如图所示。

单边循环法的实现

单边循环法和双边循环法的区别在于 partition 函数的实现。

function quickSort(arr, startIndex, endIndex) {
  // 递归结束条件: startIndex 大于或等于 endIndex 时
  if (startIndex >= endIndex) {
    return;
  }
  // 得到基准元素位置
  const pivotIndex = partition(arr, startIndex, endIndex);
  // 根据基准元素，分成两部分进行递归排序
  quickSort(arr, startIndex, pivotIndex - 1);
  quickSort(arr, pivotIndex + 1, endIndex);
}

/*
 * 分治（单边循环法）
 * @param arr 待交换的数组
 * @param startIndex 起始下标
 * @param endIndex 结束下标
 */
function partition(arr, startIndex, endIndex) {
  // 取第1个位置(也可以选择随机位置)的元素作为基准元素
  const pivot = arr[startIndex];
  let mark = startIndex;

  for (let i = startIndex + 1; i <= endIndex; i++) {
    if (arr[i] < pivot) {
      mark++;
      const temp = arr[mark];
      arr[mark] = arr[i];
      arr[i] = temp;
    }
  }

  arr[startIndex] = arr[mark];
  arr[mark] = pivot;
  return mark;
}

单边循环法的非递归实现

绝大多数的递归逻辑，都可以用栈的方式来代替。

代码中一层一层的方法调用，本身就使用了一个方法调用栈。每次进入一个新方法，就相当于入栈；每次有方法返回，就相当于出栈。

所以，可以把原本的递归实现转化成一个栈的实现，在栈中存储每一次方法调用的参数。

function quickSort(arr, startIndex, endIndex) {
  // 用一个栈来代替函数的递归栈
  const stack = [];
  // 整个数组的起止下标，以哈希的形式入栈
  const indexMap = new Map();
  indexMap.set("startIndex", startIndex);
  indexMap.set("endIndex", endIndex);
  stack.push(indexMap);

  // 循环结束条件：栈为空时
  while (stack.length) {
    // 栈顶元素出栈，得到起止下标
    const map = stack.pop();
    // 得到基准元素位置
    const pivotIndex = partition(
      arr,
      map.get("startIndex"),
      map.get("endIndex")
    );
    // 根据基准元素分成两部分, 把每一部分的起止下标入栈
    if (map.get("startIndex") < pivotIndex - 1) {
      const leftMap = new Map();
      leftMap.set("startIndex", map.get("startIndex"));
      leftMap.set("endIndex", pivotIndex - 1);
      stack.push(leftMap);
    }
    if (pivotIndex + 1 < map.get("endIndex")) {
      const rightMap = new Map();
      rightMap.set("startIndex", pivotIndex + 1);
      rightMap.set("endIndex", map.get("endIndex"));
      stack.push(rightMap);
    }
  }

  /*
   * 分治（单边循环法）
   * @param arr 待交换的数组
   * @param startIndex 起始下标
   * @param endIndex 结束下标
   */
  function partition(arr, startIndex, endIndex) {
    // 取第1个位置(也可以选择随机位置)的元素作为基准元素
    const pivot = arr[startIndex];
    let mark = startIndex;

    for (let i = startIndex + 1; i <= endIndex; i++) {
      if (arr[i] < pivot) {
        mark++;
        const temp = arr[mark];
        arr[mark] = arr[i];
        arr[i] = temp;
      }
    }

    arr[startIndex] = arr[mark];
    arr[mark] = pivot;
    return mark;
  }
}

计数排序

计数排序的思路

1. 计数排序、桶排序、基数排序都是不基于元素比较的排序算法。其中，计数排序是利用数组下标来确定元素的正确位置的。

2. 计数排序的基本思路如下：

假设数组中有 20 个随机整数，取值范围为 0~10，要求用最快的速度把这 20 个整数从小到大进行排序。

如何给这些无序的随机整数进行排序呢?

考虑到这些整数只能够在 0、1、2、3、4、5、6、7、8、9、10 这 11 个数中取值，取值范围有限。所以，可以根据这有限的范围，建立一个长度为 11 的数组。数组下标从 0 到 10，元素初始值全为 0。

假设 20 个随机整数的值如下所示。

9，3，5，4，9，1，2，7，8，1，3，6，5，3，4，0，10，9，7，9

下面就开始遍历这个无序的随机数列，每一个整数按照其值对号入座，同时，对应数组下标的元素进行加 1 操作。

例如第 1 个整数是 9，那么数组下标为 9 的元素加 1。

第 2 个整数是 3，那么数组下标为 3 的元素加 1。

继续遍历数列并修改数组......

最终，当数列遍历完毕时，数组的状态如下。

该数组中每一个下标位置的值代表数列中对应整数出现的次数。

有了这个统计结果，排序就很简单了。直接遍历数组，输出数组元素的下标值，元素的值是几，就输出几次。

0，1，1，2，3，3，3，4，4，5，5，6，7，7，8，9，9，9，9，10

显然，现在输出的数列已经是有序的了。

计数排序的实现

function countSort(arr) {
  // 1.得到数列的最大值
  let max = arr[0];
  for (let i = 0; i < arr.length; i++) {
    if (arr[i] > max) {
      max = arr[i];
    }
  }
  // 2.根据数列最大值确定统计数组的长度
  const countArr = new Array(max + 1).fill(0);
  // 3.遍历数列，填充统计数组
  for (let i = 0; i < arr.length; i++) {
    countArr[arr[i]]++;
  }
  //4.遍历统计数组，输出结果
  let index = 0;
  for (let i = 0; i < countArr.length; i++) {
    if (countArr[i] > 0) {
      arr[index++] = i;
    }
  }
}

计数排序的优化

上述的代码虽然可以实现整数的排序，但是也存在一些问题。

📌 优化点一

问题就在于，我们只以数列的最大值来决定统计数组的长度，这其实并不严谨。比如下面这个例子。

95，94，91，98，99，90，99，93，91，92

这个数列的最大值是 99，但最小的整数是 90。如果创建长度为 100 的数组，那么前面从 0 到 89 的空间位置就都浪费了!

如何解决这个问题呢？

很简单，只要不再以输入数列的最大值+1 作为统计数组的长度，而是以数列最大值-最小值+1作为统计数组的长度即可。

同时，数列的最小值作为一个偏移量，用于计算整数在统计数组中的下标。

以刚才的数列为例，统计出数组的长度为 99-90+1=10，偏移量等于数列的最小值 90。

对于第 1 个整数 95，对应的统计数组下标是 95-90 = 5，如图所示。

这确实对计数排序进行了优化。此外，朴素版的计数排序只是简单地按照统计数组的下标输出元素值，并没有真正给原始数列进行排序。

📌 优化点二

如果只是单纯地给整数排序，这样做并没有问题。但如果在现实业务里，例如给学生的考试分数进行排序，遇到相同的分数就会分不清谁是谁。

比如下面这个例子。

给出一个学生成绩表，要求按成绩从低到高进行排序，如果成绩相同，则遵循原表固有顺序。

那么，当我们填充统计数组以后，只知道有两个成绩并列为 95 分的同学，却不知道哪一个是小红，哪一个是小绿。

在这种情况下，需要稍微改变之前的逻辑，在填充完统计数组以后，对统计数组做一下变形。

仍然以刚才的学生成绩表为例，将之前的统计数组变形成下面的样子。

这是如何变形的呢?其实就是从统计数组的第 2 个元素开始，每一个元素都加上前面所有元素之和。

为什么要相加呢?

样相加的目的，是让统计数组存储的元素值，等于相应整数的最终排序位置的序号。例如下标是 9 的元素值为 5，代表原始数列的整数 9，最终的排序在第 5 位。

接下来，创建输出数组 sortedArray，长度和输入数列一致。然后从后向前遍历输入数列。

第 1 步，遍历成绩表最后一行的小绿同学的成绩。

小绿的成绩是 95 分，找到 countArray 下标是 5 的元素，值是 4，代表小绿的成绩排名位置在第 4 位。

同时，给 countArray 下标是 5 的元素值减 1，从 4 变成 3，代表下次再遇到 95 分的成绩时，最终排名是第 3。

第 2 步，遍历成绩表倒数第 2 行的小白同学的成绩。

小白的成绩是 94 分，找到 countArray 下标是 4 的元素，值是 2，代表小白的成绩排名位置在第 2 位。

同时，给 countArray 下标是 4 的元素值减 1，从 2 变成 1，代表下次再遇到 94 分的 成绩时(实际上已经遇不到了)，最终排名是第 1。

第 3 步，遍历成绩表倒数第 3 行的小红同学的成绩。

小红的成绩是 95 分，找到 countArray 下标是 5 的元素，值是 3(最初是 4，减 1 变 成了 3)，代表小红的成绩排名位置在第 3 位。

同时，给 countArray 下标是 5 的元素值减 1，从 3 变成 2，代表下次再遇到 95 分的成绩时(实际上已经遇不到了)，最终排名是第 2。

这样一来，同样是 95 分的小红和小绿就能够清楚地排出顺序了，也正因为此，优化版本的计数排序属于稳定排序。

后面的遍历过程以此类推。

function countSort(array) {
  // 1.得到数列的最大值和最小值，并算出差值d
  let min = array[0];
  let max = array[0];
  for (let i = 1; i < array.length; i++) {
    if (array[i] > max) {
      max = array[i];
    }
    if (array[i] < min) {
      min = array[i];
    }
  }
  const d = max - min;
  // 2.创建统计数组并统计对应元素的个数
  const countArray = new Array(d + 1).fill(0);
  for (let i = 0; i < array.length; i++) {
    // 数列的最小值作为一个偏移量，用于计算整数在统计数组中的下标
    countArray[array[i] - min]++;
  }
  // 3.统计数组做变形，后面的元素等于前面的元素之和
  for (let i = 1; i < countArray.length; i++) {
    countArray[i] += countArray[i - 1];
  }
  // 4.倒序遍历原始数列，从统计数组找到正确位置，输出到结果数组
  const sortedArray = new Array(array.length).fill(0);
  for (let i = array.length - 1; i >= 0; i--) {
    const offset = array[i] - min;
    sortedArray[countArray[offset] - 1] = array[i];
    countArray[offset]--;
  }
  return sortedArray;
}

计数排序的局限性

1. 当数列最大和最小值差距过大时，并不适合用计数排序。

例如给出 20 个随机整数，范围在 0 到 1 亿之间，这时如果使用计数排序，需要创建长度为 1 亿的数组。不但严重浪费空间，而且时间复杂度也会随之升高。

2. 当数列元素不是整数时，也不适合用计数排序。

如果数列中的元素都是小数，如 25.213，或 0.00 000 001 这样的数字，则无法创建对应的统计数组。这样显然无法进行计数排序。

因此，计数排序只适用于正整数并且取值范围相差不大的数组排序使用，它的排序的速度是非常可观的。

桶排序

桶排序的思路

1. 桶排序同样是一种线性时间的排序算法。类似于计数排序所创建的统计数组，桶排序需要创建若干个桶来协助排序。

2. 每一个桶（bucket）代表一个区间范围，里面可以承载一个或多个元素。

3. 桶排序的原理如下。

假设有一个非整数数列如下：

4.5，0.84，3.25，2.18，0.5

桶排序的第 1 步，就是创建这些桶，并确定每一个桶的区间范围。

具体需要建立多少个桶，如何确定桶的区间范围，有很多种不同的方式。我们这里创建的桶数量等于原始数列的元素数量，除最后一个桶只包含数列最大值外，前面各个桶的区间按照比例来确定。

区间跨度 = （最大值-最小值）/ （桶的数量 - 1）

第 2 步，遍历原始数列，把元素对号入座放入各个桶中。

第 3 步，对每个桶内部的元素分别进行排序（显然，只有第 1 个桶需要排序）。

第 4 步，遍历所有的桶，输出所有元素。

0.5，0.84，2.18，3.25，4.5

到此为止，排序结束。

桶排序的实现

// 默认情况下，我们会使用 5 个桶。桶排序在所有元素平分到各个桶中时的表现最好。
// 如果元素非常稀疏，则使用更多的桶会更好。如果元素非常密集，则使用较少的桶会更好。
function bucketSort(array, bucketSize = 5) {
  if (array.length < 2) {
    return array;
  }
  // 创建桶并将元素分布到不同的桶中
  const buckets = createBuckets(array, bucketSize);
  // 对每个桶执行插入排序算法和将所有桶合并为排序后的结果数组
  return sortBuckets(buckets);
}

// 创建桶
function createBuckets(array, bucketSize) {
  let minValue = array[0];
  let maxValue = array[0];
  for (let i = 1; i < array.length; i++) {
    if (array[i] < minValue) {
      minValue = array[i];
    } else if (array[i] > maxValue) {
      maxValue = array[i];
    }
  }
  // 计算每个桶中需要分布的元素个数
  // 计算方法是：计算数组最大值和最小值的差值并与桶的大小进行除法计算
  const bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1;
  const buckets = [];
  for (let i = 0; i < bucketCount; i++) {
    buckets[i] = [];
  }
  // 遍历数组中的每个元素，计算要将元素放到哪个桶中，并将元素插入正确的桶中
  for (let i = 0; i < array.length; i++) {
    const bucketIndex = Math.floor((array[i] - minValue) / bucketSize);
    buckets[bucketIndex].push(array[i]);
  }
  return buckets;
}

// 将每个桶进行排序
function sortBuckets(buckets) {
  const sortedArray = [];
  for (let i = 0; i < buckets.length; i++) {
    if (buckets[i] != null) {
      // 遍历每个可迭代的桶并应用插入排序，根据场景，我们还可以应用其他的排序算法，例如快速排序
      insertSort(buckets[i]);
      sortedArray.push(...buckets[i]);
    }
  }
  return sortedArray;
}

// 插入排序
function insertSort(arr) {
  for (let i = 1; i < arr.length; i++) {
    const value = arr[i];
    let j = 0; // 插入的位置
    for (j = i - 1; j >= 0 && arr[j] > value; j--) {
      arr[j + 1] = arr[j]; // 移动数据
    }
    arr[j + 1] = value; // 插入数据
  }
}

基数排序

基数排序的思路

基数排序也是一个分布式排序算法，它根据数字的有效位或基数(这也是它为什么叫基数排序)将整数分布到桶中。基数是基于数组中值的记数制的。

比如，对于十进制数，使用的基数是 10。因此，算法将会使用 10 个桶用来分布元素并且首先基于个位数字进行排序，然后基于十位数字，然后基于百位数字，以此类推。

基数排序的实现

function radixSort(array, radixBase = 10) {
  if (array.length < 2) {
    return array;
  }
  const minValue = Math.min(...array);
  const maxValue = Math.max(...array);
  // 基数排序也用来排序整数，我们就从最后一位开始排序所有的数，这个算法也可以被修改成支持排序字母字符。
  let significantDigit = 1;
  // 首先只会基于最后一位有效位对数字进行排序，在下次迭代时，我们会基于第二个有效位进行排序(十位数字)，
  // 然后是第三个有效位(百位数字)，以此类推。我们继续这个过程直到没有待排序的有效位
  // 这也是为什么我们需要知道数组中的最小值和最大值。
  // 如果数组中包含的值都在 1~9，以下循环只会执行一次。如果值都小于 99，则循环会执行第二次，以此类推。
  while ((maxValue - minValue) / significantDigit >= 1) {
    array = countingSortForRadix(array, radixBase, significantDigit, minValue);
    significantDigit *= radixBase;
  }
  return array;
}

function countingSortForRadix(array, radixBase, significantDigit, minValue) {
  let bucketsIndex;
  const buckets = [];
  const res = [];
  // 基于基数初始化桶，由于我们排序的是十进制数，那么需要 10 个桶。
  for (let i = 0; i < radixBase; i++) {
    buckets[i] = 0;
  }
  // 基于数组中数的有效位进行计数排序
  for (let i = 0; i < array.length; i++) {
    bucketsIndex = Math.floor(
      ((array[i] - minValue) / significantDigit) % radixBase
    ); // 有效位
    buckets[bucketsIndex]++; // 计数排序
  }
  // 由于我们进行的是计数排序，我们还需要计算累积结果来得到正确的计数值
  for (let i = 1; i < radixBase; i++) {
    buckets[i] += buckets[i - 1];
  }
  // 对原始数组中的每个值，我们会再次获取它的有效位并将它的值移动到 res 数组中(从 buckets 数组中减去它的计数值)
  for (let i = array.length - 1; i >= 0; i--) {
    bucketsIndex = Math.floor(
      ((array[i] - minValue) / significantDigit) % radixBase
    );
    res[--buckets[bucketsIndex]] = array[i];
  }
  return res;
}

二分查找

适用场景

使用二分查找的数据需要满足以下条件：

• 元素单调递增或递减

• 元素存在上下界

• 元素能够通过索引访问

因此，数组就很适合用二分查找，但是链表就不适合。

二分查找

题目地址 (opens new window)

var search = function(nums, target) {
  let left = 0,
    right = nums.length - 1;

  while (left <= right) {
    // const mid = (left + right) >> 1;
    const mid = left + ((right - left) >> 1);
    if (nums[mid] > target) {
      right = mid - 1;
    } else if (nums[mid] < target) {
      left = mid + 1;
    } else {
      return mid;
    }
  }

  return -1;
};

猜数字大小

题目地址 (opens new window)

var guessNumber = function(n) {
  let left = 1,
    right = n;
  while (left <= right) {
    const mid = left + ((right - left) >> 1);
    if (guess(mid) === -1) {
      right = mid - 1;
    } else if (guess(mid) === 1) {
      left = mid + 1;
    } else {
      return mid;
    }
  }
  return -1;
};

x 的平方根

题目地址 (opens new window)

// 二分查找
var mySqrt = function(x) {
  if (x <= 1) {
    return x;
  }
  let left = 1,
    right = x;
  while (left <= right) {
    const mid = left + ((right - left) >> 1); // 防止溢出
    if (mid * mid < x) {
      left = mid + 1;
    } else if (mid * mid > x) {
      right = mid - 1;
    } else {
      return mid;
    }
  }
  return right;
};

// 牛顿迭代
var mySqrt = function(x) {
  let r = x;
  while (r * r > x) {
    r = Math.floor((r + x / r) / 2);
  }
  return r;
};

搜索旋转排序数组

题目地址 (opens new window)

// 数组分割后是局部有序的，因此也可以用二分查找
var search = function(nums, target) {
  let left = 0;
  let right = nums.length - 1;

  while (left <= right) {
    // 注意这里的括号不能少
    const mid = left + ((right - left) >> 1);
    if (target === nums[mid]) {
      return mid;
    }

    // 注意这里的等号不能少
    if (nums[mid] >= nums[left]) {
      // 说明 [left, mid] 是有序的
      if (target >= nums[left] && target <= nums[mid]) {
        right = mid - 1;
      } else {
        left = mid + 1;
      }
    } else {
      // 说明 [mid, right] 是有序的
      if (target >= nums[mid] && target <= nums[right]) {
        left = mid + 1;
      } else {
        right = mid - 1;
      }
    }
  }

  return -1;
};

寻找旋转排序数组中的最小值

题目地址 (opens new window)

// 考虑数组中的最后一个元素 x：在最小值右侧的元素（不包括最后一个元素本身），它们的值一定都严格小于 x；而在最小值左侧的元素，它们的值一定都严格大于 x
var findMin = function(nums) {
  let low = 0,
    high = nums.length - 1;

  // 由于数组不包含重复元素，并且只要当前的区间长度不为 1，mid 就不会与 high 重合；而如果当区间长度为 1，说明此时可以结束二分查找了。因此不会存在 nums[mid] === nums[high] 的情况
  while (low < high) {
    const mid = low + ((high - low) >> 1);
    if (nums[mid] < nums[high]) {
      // 说明 nums[mid] 在最小值右侧，即下一步需要往 nums[mid] 的左侧区间查找
      // nums[mid] < nums[high] 时，有可能 nums[mid] 本身就是最小值，此时 mid-1 就错过了最小值，所以不要减 1
      high = mid;
    } else {
      // 说明 nums[mid] 在最小值左侧，即下一步需要往 nums[mid] 的右侧区间查找
      // nums[mid] > nums[high] 时，nums[mid] 肯定不会是最小值，所以 +1 可以过滤掉 mid 这个下标
      low = mid + 1;
    }
  }

  return nums[low];
};

有序矩阵中第 K 小的元素

题目地址 (opens new window)

var kthSmallest = function(matrix, k) {
  const n = matrix.length;
  let low = matrix[0][0],
    high = matrix[n - 1][n - 1];

  while (low <= high) {
    const mid = low + ((high - low) >> 1);
    if (countLessThanMidValue(matrix, mid) < k) {
      // 如果矩阵中小于等于中间值的元素个数小于 k，说明此时中间值小了，需要扩大范围
      low = mid + 1;
    } else {
      // 否则，说明此时中间值打了，需要缩小范围
      high = mid - 1;
    }
  }

  return low;
};

// 统计矩阵中小于等于中间值的元素个数
const countLessThanMidValue = (matrix, mid) => {
  const n = matrix.length;
  let count = 0,
    row = 0,
    col = n - 1;

  while (row < n && col >= 0) {
    // 可以先将中间值与当前行的最右边元素进行比较
    if (mid >= matrix[row][col]) {
      // 如果大于等于最右边元素，则将当前行的所有元素累加进去，即 col + 1，然后考察下一行
      count += col + 1;
      row++;
    } else {
      // 否则，继续和当前行左边的元素进行比较
      col--;
    }
  }

  return count;
};

搜索二维矩阵

题目地址 (opens new window)

// 两次二分查找
var searchMatrix = function(matrix, target) {
  // 先对矩阵的第一列进行二分查找，找到最后一个不大于目标值的元素
  const rowIndex = binarySearchFirstColumn(matrix, target);
  if (rowIndex < 0) {
    return false;
  }
  // 然后在该行中进行二分查找，看看目标元素是否存在
  return binarySearchRow(matrix[rowIndex], target);
};

const binarySearchFirstColumn = (matrix, target) => {
  let low = 0,
    high = matrix.length - 1;
  let index = 0;

  while (low <= high) {
    const mid = low + ((high - low) >> 1);
    if (matrix[mid][0] <= target) {
      index = mid;
      low = mid + 1;
    } else {
      high = mid - 1;
    }
  }

  return index;
};

const binarySearchRow = (row, target) => {
  let low = 0,
    high = row.length - 1;

  while (low <= high) {
    const mid = low + ((high - low) >> 1);
    if (row[mid] === target) {
      return true;
    } else if (row[mid] < target) {
      low = mid + 1;
    } else {
      high = mid - 1;
    }
  }

  return false;
};

分治

代码模板

def divide_conquer(problem, param1, param2, ...):

  # recursion terminator
  if problem is None:
    print_result
    return

  # prepare data
  data = prepare_data(problem)
  subproblems = split_problem(problem, data)

  # conquer subproblems
  subresult1 = self.divide_conquer(subproblems[0], p1, ...)
  subresult2 = self.divide_conquer(subproblems[1], p1, ...)
  subresult3 = self.divide_conquer(subproblems[2], p1, ...)
  ...

  # process and generate the final result
  result = process_result(subresult1, subresult2, subresult3, ...)

Pow(x, n)

题目地址 (opens new window)

以下解法的时间复杂度都是 O(logn)。

var myPow = function(x, n) {
  if (!n) return 1;

  // n 为负数时，x 的 n 次方等于 1 除以 x 的 -n 次方
  if (n < 0) return 1 / myPow(x, -n);

  // n 为奇数时，n-1 就是偶数，传给下一层，此时就留到下一次递归的时候再通过偶数分治进行计算
  if (n % 2) return x * myPow(x, n - 1);

  // n 为偶数时，使用分治，一分为二进行计算
  return myPow(x * x, n / 2);
};

var myPow = function(x, n) {
  if (n < 0) {
    x = 1 / x;
    n = -n;
  }

  let result = 1;
  while (n) {
    if (n & 1) result *= x;
    x *= x;
    n >>= 1;
  }

  return result;
};

多数元素

题目地址 (opens new window)

方法一：两层循环暴力破解，一层用来遍历，一层用来计数。时间复杂度为：O(n^2)。

var majorityElement = function(nums) {
  let middle = nums.length / 2;
  for (let i = 0; i < nums.length; i++) {
    let times = 1; // 这一行要放在第一层循环内，如果放在循环外会出错
    for (let j = i + 1; j < nums.length; j++) {
      if (nums[i] === nums[j]) {
        times++;
      }
    }
    if (times > middle) {
      return nums[i];
    }
  }
};

方法二：使用 map 来存储每个数出现的次数，这样只需要一次遍历。时间复杂度为：O(n)。

var majorityElement = function(nums) {
  let map = new Map();

  for (let num of nums) {
    if (map.has(num)) {
      map.set(num, map.get(num) + 1);
    } else {
      map.set(num, 1);
    }

    if (map.get(num) > nums.length / 2) return num;
  }
};

方法三：先排序，然后取 n/2 处的数字就是多数元素。时间复杂度为：O(nlogn)。

var majorityElement = function(nums) {
  nums.sort((a, b) => a - b);
  return nums[Math.floor(nums.length / 2)];
};

方法四：分治法。时间复杂度为：O(nlogn)。

var majorityElement = function(nums) {
  const helper = (start, end) => {
    if (start === end) return nums[start];

    // 拆分成更小的区间，一分为二
    let mid = Math.floor((start + end) / 2);

    let left = helper(start, mid);
    let right = helper(mid + 1, end);

    if (left === right) return left;

    let leftCount = getCount(left, start, end); // 统计区间内 left 的个数
    let rightCount = getCount(right, start, end); // 统计区间内 right 的个数

    return leftCount > rightCount ? left : right; // 返回 left 和 right 中个数多的那个
  };

  //统计 start 到 end 之间 num 的数量
  const getCount = (num, start, end) => {
    let count = 0;
    for (let i = start; i <= end; i++) {
      if (nums[i] === num) count++;
    }
    return count;
  };

  return helper(0, nums.length - 1);
};

方法五：摩尔投票法。时间复杂度为：O(n)。

var majorityElement = function(nums) {
  let res = nums[0],
    count = 1;
  for (let i = 1; i < nums.length; i++) {
    if (count === 0) {
      res = nums[i];
      count = 1;
    } else if (nums[i] === res) {
      count++;
    } else {
      count--;
    }
  }
  return res;
};

动态规划

动态规划的思路

1. 递归 + 记忆化 -> 递推

2. 状态的定义：opt[n]，dp[n]

3. 状态转移方程：opt[n] = best_of(opt[n - 1], opt[n - 2], ...)

4. 最优子结构

动态规划、回溯、贪心对比

• 回溯（递归）- 重复计算

• 贪心 - 永远局部最优

• 动态规划 - 记录局部最优子结构/多种记录值

斐波那契数列

题目地址 (opens new window)

拜托，面试别再问我斐波那契数列了！！！ (opens new window)

const fib = (n) => {
  return n <= 1 ? n : fib(n - 1) + fib(n - 2);
};

const fib = (n) => {
  if (n <= 1) return n;
  const dp = [];
  dp[0] = 0;
  dp[1] = 1;
  for (let i = 2; i <= n; i++) {
    dp[i] = dp[i - 1] + dp[i - 2];
  }
  return dp[n];
};

const fib = (n) => {
  if (n <= 1) return n;
  let dp0 = 0;
  let dp1 = 0;
  let dp = 1;
  for (let i = 2; i <= n; i++) {
    dp0 = dp1;
    dp1 = dp;
    dp = dp0 + dp1;
  }
  return dp;
};

爬楼梯

题目地址 (opens new window)

const climbStairs = (n) => {
  const dp = [];
  dp[0] = 1;
  dp[1] = 1;
  for (let i = 2; i <= n; i++) {
    dp[i] = dp[i - 1] + dp[i - 2];
  }
  return dp[n];
};

const climbStairs = function(n) {
  let dp0 = 0;
  let dp1 = 0;
  let dp = 1;
  for (let i = 1; i <= n; i++) {
    dp0 = dp1;
    dp1 = dp;
    dp = dp0 + dp1;
  }
  return dp;
};

打家劫舍

题目地址 (opens new window)

var rob = function(nums) {
  const n = nums.length;
  if (n === 0) return 0;
  if (n === 1) return nums[0];
  const sum = [];
  sum[0] = nums[0];
  sum[1] = Math.max(nums[0], nums[1]);
  for (let i = 2; i < n; i++) {
    sum[i] = Math.max(sum[i - 2] + nums[i], sum[i - 1]);
  }
  return sum[n - 1];
};

var rob = function(nums) {
  const n = nums.length;
  if (n === 0) return 0;
  if (n === 1) return nums[0];
  let first = nums[0];
  let second = Math.max(nums[0], nums[1]);
  for (let i = 2; i < n; i++) {
    let temp = second;
    second = Math.max(first + nums[i], second);
    first = temp;
  }
  return second;
};

三角形的最小路径和

题目地址 (opens new window)

const minimumTotal = (triangle) => {
  for (let i = triangle.length - 2; i >= 0; i--) {
    for (let j = 0; j < triangle[i].length; j++) {
      triangle[i][j] =
        Math.min(triangle[i + 1][j], triangle[i + 1][j + 1]) + triangle[i][j];
    }
  }
  return triangle[0][0];
};

const minimumTotal = (triangle) => {
  let dp = new Array(triangle.length + 1).fill(0);
  for (let i = triangle.length - 1; i >= 0; i--) {
    for (let j = 0; j < triangle[i].length; j++) {
      dp[j] = Math.min(dp[j], dp[j + 1]) + triangle[i][j];
    }
  }
  return dp[0];
};

最大子数组和

题目地址 (opens new window)

var maxSubArray = function(nums) {
  let sum = 0; // 只用一个变量 sum 来维护对于当前 f(i) 的 f(i-1) 的值，从而将空间复杂度降为 O(1)
  let res = nums[0];

  for (let i = 0; i < nums.length; i++) {
    // 状态转移方程：f(i) = max{f(i−1) + nums[i], nums[i]}
    sum = Math.max(sum + nums[i], nums[i]);
    res = Math.max(res, sum);
  }

  return res;
};

乘积最大子数组

题目地址 (opens new window)

var maxProduct = function(nums) {
  const n = nums.length;
  const min = new Array(n).fill(0);
  const max = new Array(n).fill(0);
  min[0] = nums[0];
  max[0] = nums[0];

  for (let i = 1; i < n; i++) {
    min[i] = Math.min(min[i - 1] * nums[i], max[i - 1] * nums[i], nums[i]);
    max[i] = Math.max(max[i - 1] * nums[i], min[i - 1] * nums[i], nums[i]);
  }

  return Math.max(...max);
};

const maxProduct = (nums) => {
  const dp = new Array(2).fill(0).map(() => new Array(2).fill(0));
  dp[0][0] = nums[0]; // dp[i][0] 表示数组中下标从 0 到 i 的连续子数组的最小值，负数
  dp[0][1] = nums[0]; // dp[i][1] 表示数组中下标从 0 到 i 的连续子数组的最大值，正数
  let max = nums[0];

  for (let i = 1; i < nums.length; i++) {
    const x = i % 2,
      y = (i - 1) % 2; // 滚动数组，因此上面只需要申请空间为 2 的二维数组就行了
    dp[x][0] = Math.min(dp[y][0] * nums[i], dp[y][1] * nums[i], nums[i]);
    dp[x][1] = Math.max(dp[y][1] * nums[i], dp[y][0] * nums[i], nums[i]);
    max = Math.max(max, dp[x][1]);
  }

  return max;
};

const maxProduct = (nums) => {
  let curMin = nums[0];
  let curMax = nums[0];
  let tempMin = 0;
  let tempMax = 0;
  let max = nums[0];

  for (let i = 1; i < nums.length; i++) {
    tempMin = curMin * nums[i];
    tempMax = curMax * nums[i];
    curMin = Math.min(tempMin, tempMax, nums[i]);
    curMax = Math.max(tempMax, tempMin, nums[i]);
    max = Math.max(max, curMax);
  }

  return max;
};

const maxProduct = (nums) => {
  let max = nums[0],
    curMax = nums[0],
    curMin = nums[0];
  for (let i = 1; i < nums.length; i++) {
    if (nums[i] < 0) {
      [curMax, curMin] = [curMin, curMax];
    }
    curMax = Math.max(curMax * nums[i], nums[i]);
    curMin = Math.min(curMin * nums[i], nums[i]);
    max = Math.max(curMax, max);
  }
  return max;
};

买卖股票的最佳时机

题目地址 (opens new window)

const maxProfit = (prices) => {
  let minPrice = Number.MAX_VALUE;
  let maxProfit = 0;
  for (let i = 0; i < prices.length; i++) {
    maxProfit = Math.max(prices[i] - minPrice, maxProfit);
    minPrice = Math.min(prices[i], minPrice);
  }
  return maxProfit;
};

买卖股票的最佳时机 II

题目地址 (opens new window)

// 动态规划
const maxProfit = (prices) => {
  const n = prices.length;
  const dp = new Array(n).fill(0).map(() => new Array(2).fill(0));
  dp[0][0] = 0;
  dp[0][1] = -prices[0];
  for (let i = 1; i < n; i++) {
    dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
    dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
  }
  return dp[n - 1][0];
};

// 动态规划 + 空间优化
const maxProfit = (prices) => {
  let dp0 = 0;
  let dp1 = -prices[0];
  for (let i = 1; i < prices.length; i++) {
    const temp0 = Math.max(dp0, dp1 + prices[i]);
    const temp1 = Math.max(dp1, dp0 - prices[i]);
    dp0 = temp0;
    dp1 = temp1;
  }
  return dp0;
};

// 贪心
const maxProfit = (prices) => {
  let profit = 0;
  for (let i = 0; i < prices.length; i++) {
    if (prices[i] > prices[i - 1]) {
      profit += prices[i] - prices[i - 1];
    }
  }
  return profit;
};

买卖股票的最佳时机 III

题目地址 (opens new window)

const maxProfit = (prices) => {
  const n = prices.length;
  const dp = new Array(n)
    .fill(0)
    .map(() => new Array(3).fill(0).map(() => new Array(2).fill(0)));
  for (let i = 0; i <= 2; i++) {
    dp[0][i][0] = 0;
    dp[0][i][1] = -prices[0];
  }
  for (let i = 1; i < n; i++) {
    dp[i][0][0] = 0;
    dp[i][0][1] = Math.max(dp[i - 1][0][1], dp[i - 1][0][0] - prices[i]);
  }
  for (let i = 1; i < n; i++) {
    for (let j = 1; j <= 2; j++) {
      dp[i][j][0] = Math.max(dp[i - 1][j][0], dp[i - 1][j - 1][1] + prices[i]);
      dp[i][j][1] = Math.max(dp[i - 1][j][1], dp[i - 1][j][0] - prices[i]);
    }
  }
  return dp[n - 1][2][0];
};

const maxProfit = (prices) => {
  let buy1 = -prices[0]; // 进行第一次买操作获得的最大利润
  let sell1 = 0; // 进行一次买操作和一次卖操作获得的最大利润，即完成第一笔交易
  let buy2 = -prices[0]; // 在完成一笔交易的前提下，进行第二次买操作获得的最大利润
  let sell2 = 0; // 进行第二次卖操作获得的最大利润，即完成第二笔交易
  for (let i = 1; i < prices.length; i++) {
    buy1 = Math.max(buy1, -prices[i]);
    sell1 = Math.max(sell1, buy1 + prices[i]);
    buy2 = Math.max(buy2, sell1 - prices[i]);
    sell2 = Math.max(sell2, buy2 + prices[i]);
  }
  return sell2;
};

买卖股票的最佳时机 IV

题目地址 (opens new window)

const maxProfit = (k, prices) => {
  const n = prices.length;
  const dp = new Array(n)
    .fill(0)
    .map(() => new Array(k + 1).fill(0).map(() => new Array(2).fill(0)));
  for (let i = 0; i <= k; i++) {
    dp[0][i][0] = 0;
    dp[0][i][1] = -prices[0];
  }
  for (let i = 1; i < n; i++) {
    dp[i][0][0] = 0;
    dp[i][0][1] = Math.max(dp[i - 1][0][1], dp[i - 1][0][0] - prices[i]);
  }
  for (let i = 1; i < n; i++) {
    for (let j = 1; j <= k; j++) {
      dp[i][j][0] = Math.max(dp[i - 1][j][0], dp[i - 1][j - 1][1] + prices[i]);
      dp[i][j][1] = Math.max(dp[i - 1][j][1], dp[i - 1][j][0] - prices[i]);
    }
  }
  return dp[n - 1][k][0];
};

最佳买卖股票时机含冷冻期

题目地址 (opens new window)

const maxProfit = (prices) => {
  const n = prices.length;
  const dp = new Array(n).fill(0).map(() => new Array(3).fill(0));
  dp[0][0] = -prices[0];
  for (let i = 1; i < n; i++) {
    dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][2] - prices[i]); // 手上持有股票的最大收益
    dp[i][1] = dp[i - 1][0] + prices[i]; // 手上不持有股票，并且处于冷冻期中的累计最大收益
    dp[i][2] = Math.max(dp[i - 1][1], dp[i - 1][2]); // 手上不持有股票，并且不在冷冻期中的累计最大收益
  }
  return Math.max(dp[n - 1][1], dp[n - 1][2]);
};

const maxProfit = (prices) => {
  let dp0 = -prices[0];
  let dp1 = 0;
  let dp2 = 0;
  for (let i = 1; i < prices.length; i++) {
    const temp0 = Math.max(dp0, dp2 - prices[i]);
    const temp1 = dp0 + prices[i];
    const temp2 = Math.max(dp1, dp2);
    dp0 = temp0;
    dp1 = temp1;
    dp2 = temp2;
  }
  return Math.max(dp1, dp2);
};

买卖股票的最佳时机含手续费

题目地址 (opens new window)

const maxProfit = (prices, fee) => {
  const n = prices.length;
  const dp = new Array(n).fill(0).map(() => new Array(2).fill(0));
  dp[0][0] = 0;
  dp[0][1] = -prices[0];
  for (let i = 1; i < n; i++) {
    dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i] - fee);
    dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
  }
  return dp[n - 1][0];
};

const maxProfit = (prices, fee) => {
  let dp0 = 0;
  let dp1 = -prices[0];
  for (let i = 1; i < prices.length; i++) {
    const temp0 = Math.max(dp0, dp1 + prices[i] - fee);
    const temp1 = Math.max(dp1, dp0 - prices[i]);
    dp0 = temp0;
    dp1 = temp1;
  }
  return dp0;
};

const maxProfit = (prices, fee) => {
  let [dp0, dp1] = [0, -prices[0]];
  for (let i = 1; i < prices.length; i++) {
    [dp0, dp1] = [
      Math.max(dp0, dp1 + prices[i] - fee),
      Math.max(dp1, dp0 - prices[i])
    ];
  }
  return dp0;
};

最长递增子序列

题目地址 (opens new window)

// 动态规划
var lengthOfLIS = function(nums) {
  const n = nums.length;
  if (n <= 1) return n;
  let res = 1;
  const dp = [];
  dp[0] = 1;
  for (let i = 1; i < n; i++) {
    dp[i] = 1;
    for (let j = 0; j < i; j++) {
      if (nums[i] > nums[j]) {
        dp[i] = Math.max(dp[i], dp[j] + 1);
      }
    }
    res = Math.max(res, dp[i]);
  }
  return res;
};

// 二分查找
var lengthOfLIS = function(nums) {
  const n = nums.length;
  if (n <= 1) return n;
  const res = [nums[0]];
  for (let i = 1; i < n; i++) {
    if (nums[i] > res[res.length - 1]) {
      res.push(nums[i]);
    } else {
      let left = 0;
      let right = res.length - 1;
      while (left < right) {
        let mid = left + ((right - left) >> 1);
        if (nums[i] > res[mid]) {
          left = mid + 1;
        } else {
          right = mid;
        }
      }
      res[left] = nums[i];
    }
  }
  return res.length;
};

最长回文子序列

题目地址 (opens new window)

var longestPalindromeSubseq = function(s) {
  const n = s.length;
  const dp = new Array(n).fill(0).map(() => new Array(n).fill(0));

  for (let i = 0; i < n; i++) {
    dp[i][i] = 1;
  }

  for (let i = n - 1; i >= 0; i--) {
    for (let j = i + 1; j < n; j++) {
      if (s[i] === s[j]) {
        dp[i][j] = dp[i + 1][j - 1] + 2;
      } else {
        dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
      }
    }
  }

  return dp[0][n - 1];
};

零钱兑换

题目地址 (opens new window)

const coinChange = (coins, amount) => {
  if (!amount) return 0;
  const dp = new Array(amount + 1).fill(amount + 1);
  dp[0] = 0;
  for (let i = 1; i <= amount; i++) {
    for (let j = 0; j < coins.length; j++) {
      if (i >= coins[j]) {
        dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1);
      }
    }
  }
  return dp[amount] > amount ? -1 : dp[amount];
};

编辑距离

题目地址 (opens new window)

const minDistance = (word1, word2) => {
  const m = word1.length;
  const n = word2.length;
  const dp = Array.from(new Array(m + 1), () => new Array(n + 1).fill(0));
  for (let i = 1; i <= m; i++) {
    dp[i][0] = i;
  }
  for (let j = 1; j <= n; j++) {
    dp[0][j] = j;
  }
  // dp[i][j] 表示将 word1 的前 i 个字符变成 word2 的前 j 个字符需要的最少操作数
  for (let i = 1; i <= m; i++) {
    for (let j = 1; j <= n; j++) {
      if (word1[i - 1] === word2[j - 1]) {
        dp[i][j] = dp[i - 1][j - 1];
      } else {
        dp[i][j] = 1 + Math.min(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]);
      }
    }
  }
  return dp[m][n];
};

贪心

贪心算法的核心：在对问题求解时，总是做出在当前看来最好的选择。

贪心算法的适用场景：

问题能够分解成⼦问题来解决，⼦问题的最优解能递推到最终问题的最优解。这种⼦问题最优解成为最优⼦结构。

贪⼼算法与动态规划的不同在于它对每个⼦问题的解决⽅案都做出选择，不能回退。

动态规划则会保存以前的运算结果，并根据以前的结果对当前进⾏选择，有回退功能。

买卖股票的最佳时机 II

题目地址 (opens new window)

关键条件：只能持有 1 股、买卖无数次、无交易手续费

方法一：贪心算法。时间复杂度为：O(n)。

var maxProfit = function(prices) {
  let profit = 0;
  for (let i = 0; i < prices.length; i++) {
    // 只要当天的股价大于前一天的股价，就卖出，累计利润
    if (prices[i] > prices[i - 1]) {
      profit += prices[i] - prices[i - 1];
    }
  }
  return profit;
};

方法二：动态规划。时间复杂度为：O(n)。

var maxProfit = function(prices) {
  // dp0 表示第 i 天交易结束后手里没有股票的最大利润，dp1 表示第 i 天交易结束后手里有一支股票的最大利润
  // 它们的初始值为第 0 天交易结束后的最大利润
  let dp0 = 0,
    dp1 = -prices[0];
  for (let i = 1; i < prices.length; ++i) {
    // 如果第 i 天交易完后手里没有股票，那么可能的转移状态为前一天已经没有股票或者前一天结束的时候手里持有一支股票，此时需要将其卖出，获取 prices[i] 的收益
    let newDp0 = Math.max(dp0, dp1 + prices[i]);
    // 如果第 i 天交易完后手里有一支股票，那么可能的转移状态为前一天已经持有一支股票或者前一天结束的时候手里没有股票，此时需要买入一支，并减少 prices[i] 的收益
    let newDp1 = Math.max(dp1, dp0 - prices[i]);
    dp0 = newDp0;
    dp1 = newDp1;
  }
  return dp0;
};

广度优先搜索（BFS）和深度优先搜索（DFS）

用于在树或者图中寻找特定节点。

BFS 代码模板

generate_related_nodes 函数中会做两件事：

• 找到下一个节点；

• 判断该节点没有被访问过，才取出来。

visited = set()
def BFS(graph, start, end):
  queue = []
  queue.append([start])
  visited.add(start)

  while queue:
    node = queue.pop()
    visited.add(node)

    process(node)

    nodes = generate_related_nodes(node)
    queue.push(nodes)

  # other processing work
  ...

DFS 代码模板

一般推荐使用递归写法，面试中也是。

递归写法：

visited = set()
def DFS(node, visited):
  visited.add(node)
  # process current node here
  ...
  for next_node in node.children():
    if not next_node in visited:
      DFS(next_node, visited)

非递归写法：

def DFS(self, tree):
  if tree.root is None:
    return []

  visited, stack = [], [tree.root]

  while stack:
    node = stack.pop()
    visited.add(node)

    process(node)
    nodes = generate_related_nodes(node)
    tack.push(node)

  # other processing work
  ...

二叉树的层序遍历

题目地址 (opens new window)

// BFS
var levelOrder = function(root) {
  if (root === null) return [];
  const res = [],
    queue = [root];
  while (queue.length) {
    const currentLevel = [],
      levelSize = queue.length;
    for (let i = 0; i < levelSize; i++) {
      const node = queue.shift();
      currentLevel.push(node.val);
      if (node.left) queue.push(node.left);
      if (node.right) queue.push(node.right);
    }
    res.push(currentLevel);
  }
  return res;
};

// 使用 DFS 中的中序遍历，增加一个层级的变量，由于闭包的特性，在每个函数调用中的层级都是自己当前的层级
var levelOrder = function(root) {
  const res = [];
  const traverse = (node, level) => {
    if (node !== null) {
      traverse(node.left, level + 1);
      res[level] ? res[level].push(node.val) : (res[level] = [node.val]);
      traverse(node.right, level + 1);
    }
  };
  traverse(root, 0);
  return res;
};

二叉树的最大深度

题目地址 (opens new window)

// DFS
var maxDepth = function(root) {
  return root === null
    ? 0
    : Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
};

// BFS
var maxDepth = function(root) {
  if (root === null) return 0;
  let queue = [root];
  let depth = 0;
  while (queue.length) {
    let levelSize = queue.length;
    for (let i = 0; i < levelSize; i++) {
      const node = queue.shift();
      if (node.left) queue.push(node.left);
      if (node.right) queue.push(node.right);
    }
    depth++;
  }
  return depth;
};

二叉树的最小深度

题目地址 (opens new window)

// DFS
var minDepth = function(root) {
  if (root === null) return 0;
  let left = minDepth(root.left);
  let right = minDepth(root.right);
  return left === 0 || right === 0
    ? left + right + 1
    : Math.min(left, right) + 1;
};

// BFS
var minDepth = function(root) {
  if (root == null) return 0;
  let queue = [root];
  let depth = 1; // root 本身就是一层，所以深度初始化为 1
  while (queue.length) {
    let levelSize = queue.length;
    while (levelSize--) {
      let node = queue.shift();
      // 判断是当前否是叶子节点
      if (node.left == null && node.right == null) {
        return depth;
      }
      // 如果不是叶子结点，就将其相邻节点加入队列
      if (node.left) queue.push(node.left);
      if (node.right) q.push(node.right);
    }
    depth++;
  }
  return depth;
};

岛屿数量

题目地址 (opens new window)

// DFS
const dfs = (grid, r, c) => {
  // 去除不合法的以及不是岛屿的点
  if (
    r < 0 ||
    r >= grid.length ||
    c < 0 ||
    c > grid[0].length ||
    grid[r][c] !== "1"
  ) {
    return;
  }
  // 访问过的岛屿置为 '0'
  grid[r][c] = "0";
  // 遍历该点的上下左右 4 个方向的点
  dfs(grid, r - 1, c);
  dfs(grid, r + 1, c);
  dfs(grid, r, c - 1);
  dfs(grid, r, c + 1);
};

const numIslands = (grid) => {
  let count = 0;
  for (let i = 0; i < grid.length; i++) {
    for (let j = 0; j < grid[0].length; j++) {
      if (grid[i][j] === "1") {
        dfs(grid, i, j);
        count++;
      }
    }
  }
  return count;
};

// DFS
const dfs = (grid, r, c) => {
  // 去除不合法的以及不是岛屿的点
  if (
    r < 0 ||
    r >= grid.length ||
    c < 0 ||
    c > grid[0].length ||
    grid[r][c] !== "1"
  ) {
    return;
  }
  // 访问过的岛屿置为 '0'
  grid[r][c] = "0";
  // 遍历该点的上下左右 4 个方向的点
  const dx = [-1, 1, 0, 0];
  const dy = [0, 0, -1, 1];
  for (let i = 0; i < 4; i++) {
    dfs(grid, r + dy[i], c + dx[i]);
  }
};

const numIslands = (grid) => {
  let count = 0;
  for (let i = 0; i < grid.length; i++) {
    for (let j = 0; j < grid[0].length; j++) {
      if (grid[i][j] === "1") {
        dfs(grid, i, j);
        count++;
      }
    }
  }
  return count;
};

// BFS
const bfs = (grid, r, c) => {
  const queue = [];
  queue.push([r, c]);
  while (queue.length) {
    [r, c] = queue.pop();
    if (
      r >= 0 &&
      r < grid.length &&
      c >= 0 &&
      c < grid[0].length &&
      grid[r][c] === "1"
    ) {
      grid[r][c] = "0";
      const dx = [-1, 1, 0, 0];
      const dy = [0, 0, -1, 1];
      for (let i = 0; i < 4; i++) {
        queue.push([r + dy[i], c + dx[i]]);
      }
    }
  }
};

const numIslands = (grid) => {
  let count = 0;
  for (let i = 0; i < grid.length; i++) {
    for (let j = 0; j < grid[0].length; j++) {
      if (grid[i][j] === "1") {
        bfs(grid, i, j);
        count++;
      }
    }
  }
  return count;
};

递归、剪枝和回溯

递归代码模板

def recursion(level, param1, param2, ...):

  # recursion terminator
  if level > MAX_LEVEL:
    print_result
    return

  # process logic in current level
  process_data(level, data...)

  # drill down
  self.recursion(level + 1, p1, ...)

  # reverse the current level status if needed
  reverse_status(level)

回溯解题思路

1. 用 for 循环去枚举出所有的选择。

2. 做出一个选择。

3. 基于这个选择，继续往下选择（递归）。

4. 上面的递归结束了，撤销这个选择，进入 for 循环的下一次迭代。

括号生成

题目地址 (opens new window)

var generateParenthesis = function(n) {
  const res = [];

  const helper = (left, right, s) => {
    if (left === n && right === n) {
      res.push(s);
      return;
    }
    // 如果左括号数量不大于 n，可以放一个左括号
    if (left < n) {
      helper(left + 1, right, s + "(");
    }
    // 如果右括号数量小于左括号的数量，可以放一个右括号
    if (right < left) {
      helper(left, right + 1, s + ")");
    }
  };

  helper(0, 0, "");

  return res;
};

var generateParenthesis = function(n) {
  const res = [];

  const helper = (left, right, s) => {
    if (left === 0 && right === 0) {
      res.push(s);
      return;
    }
    if (left > 0) {
      helper(left - 1, right, s + "(");
    }
    if (right > left) {
      helper(left, right - 1, s + ")");
    }
  };

  helper(n, n, "");

  return res;
};

子集

题目地址 (opens new window)

var subsets = function(nums) {
  const res = [];

  const helper = (i, arr) => {
    if (i === nums.length) {
      res.push(arr);
      return;
    }
    // 取当前的元素
    arr.push(nums[i]);
    helper(i + 1, arr);
    arr.pop();
    // 不取当前的元素
    helper(i + 1, arr);
  };

  helper(0, []);

  return res;
};

子集 II

题目地址 (opens new window)

var subsetsWithDup = function(nums) {
  const res = [];
  nums.sort();

  const helper = (start, arr) => {
    res.push(arr.slice());
    if (start === nums.length) {
      return;
    }
    for (let i = start; i < nums.length; i++) {
      if (i > start && nums[i - 1] === nums[i]) {
        continue;
      }
      arr.push(nums[i]);
      helper(i + 1, arr);
      arr.pop();
    }
  };

  helper(0, []);

  return res;
};

组合

题目地址 (opens new window)

var combine = function(n, k) {
  const res = [];

  // start 是选择的起点，arr 是当前构建的组合
  const helper = (start, arr) => {
    if (arr.length === k) {
      res.push([...arr]); // 将当前符合的组合推入结果中
      return;
    }
    for (let i = start; i <= n; i++) {
      // 遍历所有选择
      arr.push(i); // 当前选择
      helper(i + 1, arr); // 继续选择
      arr.pop(); // 撤销当前选择
    }
  };

  helper(1, []);

  return res;
};

组合总和

题目地址 (opens new window)

var combinationSum = function(candidates, target) {
  const res = [];

  const helper = (start, arr, sum) => {
    if (sum >= target) {
      if (sum === target) {
        res.push(arr.slice());
      }
      return;
    }
    for (let i = start; i < candidates.length; i++) {
      arr.push(candidates[i]);
      helper(i, arr, sum + candidates[i]);
      arr.pop();
    }
  };

  helper(0, [], 0);

  return res;
};

组合总和 II

题目地址 (opens new window)

var combinationSum2 = function(candidates, target) {
  const res = [];
  candidates.sort();

  const helper = (start, arr, sum) => {
    if (sum >= target) {
      if (sum === target) {
        res.push(arr.slice());
      }
      return;
    }
    for (let i = start; i < candidates.length; i++) {
      if (i > start && candidates[i - 1] === candidates[i]) {
        continue;
      }
      arr.push(candidates[i]);
      helper(i + 1, arr, sum + candidates[i]);
      arr.pop();
    }
  };

  helper(0, [], 0);

  return res;
};

组合总和 III

题目地址 (opens new window)

var combinationSum3 = function(k, n) {
  const res = [];

  const helper = (start, arr, sum) => {
    if (arr.length === k) {
      if (sum === n) {
        res.push(arr.slice());
      }
      return;
    }
    for (let i = start; i <= 9; i++) {
      arr.push(i);
      helper(i + 1, arr, sum + i);
      arr.pop();
    }
  };

  helper(1, [], 0);

  return res;
};

全排列

题目地址 (opens new window)

var permute = function(nums) {
  const res = [];

  const helper = (arr) => {
    if (arr.length === nums.length) {
      res.push(arr.slice());
      return;
    }
    for (let i = 0; i < nums.length; i++) {
      if (!arr.includes(nums[i])) {
        arr.push(nums[i]);
        helper(arr);
        arr.pop();
      }
    }
  };

  helper([]);

  return res;
};

全排列 II

题目地址 (opens new window)

var permuteUnique = function(nums) {
  const res = [];
  const visited = [];
  nums.sort();

  const helper = (arr) => {
    if (arr.length === nums.length) {
      res.push(arr.slice());
      return;
    }
    for (let i = 0; i < nums.length; i++) {
      if (visited[i] || (i > 0 && nums[i - 1] === nums[i] && !visited[i - 1])) {
        continue;
      }
      arr.push(nums[i]);
      visited[i] = 1;
      helper(arr);
      arr.pop();
      visited[i] = 0;
    }
  };

  helper([]);

  return res;
};

N 皇后

题目地址 (opens new window)

const solveNQueens = (n) => {
  const board = new Array(n);
  for (let i = 0; i < n; i++) {
    board[i] = new Array(n).fill("."); // 创建棋盘
  }

  const cols = new Set(); // 列
  const leftDiag = new Set(); // 左对角线
  const rightDiag = new Set(); // 右对角线
  const res = [];

  const helper = (row) => {
    if (row === n) {
      const stringsBoard = board.slice();
      for (let i = 0; i < n; i++) {
        stringsBoard[i] = stringsBoard[i].join("");
      }
      res.push(stringsBoard);
      return;
    }
    for (let col = 0; col < n; col++) {
      // 如果当前点的所在的列和左右对角线任意一处有皇后，那么跳过该点
      if (cols.has(col) || leftDiag.has(row + col) || rightDiag.has(row - col))
        continue;
      // 放置皇后，并将对应的列和左右对角线记录下来
      board[row][col] = "Q";
      cols.add(col);
      rightDiag.add(row - col);
      leftDiag.add(row + col);

      // 递归下一行
      helper(row + 1);

      // 恢复现场，撤销该点的皇后，并删掉对应的列和左右对角线记录
      board[row][col] = ".";
      cols.delete(col);
      rightDiag.delete(row - col);
      leftDiag.delete(row + col);
    }
  };
  helper(0);
  return res;
};

N 皇后 II

题目地址 (opens new window)

const totalNQueens = (n) => {
  const cols = new Set();
  const leftDiag = new Set();
  const rightDiag = new Set();
  let count = 0;

  const helper = (row) => {
    if (row >= n) return count++;

    for (let col = 0; col < n; col++) {
      if (cols.has(col) || leftDiag.has(row + col) || rightDiag.has(row - col))
        continue;

      cols.add(col);
      leftDiag.add(row + col);
      rightDiag.add(row - col);

      helper(row + 1);

      cols.delete(col);
      leftDiag.delete(row + col);
      rightDiag.delete(row - col);
    }
  };
  helper(0);

  return count;
};

cosnt totalNQueens = (n) => {
  let count = 0;

  const dfs = (row, col, leftDiag, rightDiag) => {
    if (row >= n) {
      count++;
      return;
    }

    // 得到当前层所有的空位，即可以放置皇后的位置；同时将这些空位转成 1，已经放置了皇后的位置转成 0
    let bits = (~(col | leftDiag | rightDiag)) & ((1 << n) - 1);

    while (bits) {
      const one = bits & -bits; // 得到最低位的 1
      dfs(row + 1, col | one, (leftDiag | one) << 1, (rightDiag | one) >> 1); // 更新行、列和左右对角线，进行新一轮的遍历
      bits = bits & (bits - 1); // 去掉最低位的 1
    }
  };

  dfs(0, 0, 0, 0);
  return count;
};

单词搜索

题目地址 (opens new window)

var exist = function(board, word) {
  const row = board.length;
  const col = board[0].length;
  const visited = new Array(row); // 与 board 一样大的二维数组，用于标记当前点是否访问过
  for (let i = 0; i < row; i++) {
    visited[i] = new Array(col);
  }

  const dfs = function(r, c, i) {
    // r 是当前点的横坐标，c 是当前点的纵坐标，i 是当前检查的单词中的字符索引
    if (i === word.length) {
      // 递归出口，遍历完当前检查的单词
      return true;
    }
    if (r < 0 || r >= row || c < 0 || c >= col) {
      // 当前点坐标越界
      return false;
    }
    if (visited[r][c] || board[r][c] !== word[i]) {
      // 当前点已经访问过或者它不是目标点
      return false;
    }
    visited[r][c] = true; // 标记当前点已被访问过
    const next =
      dfs(r - 1, c, i + 1) ||
      dfs(r + 1, c, i + 1) ||
      dfs(r, c - 1, i + 1) ||
      dfs(r, c + 1, i + 1); // 检查当前点的上下左右四个点能否找到下一个字符
    if (next) {
      return true;
    }
    visited[r][c] = false; // 如果不能找到下一个字符，需要撤销当前点的访问状态
    return false;
  };

  for (let i = 0; i < row; i++) {
    for (let j = 0; j < col; j++) {
      if (board[i][j] === word[0] && dfs(i, j, 0)) {
        // 找到递归起点，并且递归结果为真
        return true;
      }
    }
  }

  return false;
};

单词搜索 II

题目地址 (opens new window)

// 回溯 + 字典树
const findWords = (board, words) => {
  const row = board.length;
  const col = board[0].length;
  const res = [];

  // 构建字典树
  const getTrie = (words) => {
    let root = Object.create(null);
    for (const word of words) {
      let node = root;
      for (let c of word) {
        if (!node[c]) {
          node[c] = Object.create(null);
        }
        node = node[c];
      }
      node.word = word;
    }
    return root;
  };

  const dfs = (r, c, trie) => {
    if (trie.word) {
      res.push(trie.word);
      trie.word = null;
    }

    // 边界条件
    if (r < 0 || r >= row || c < 0 || c >= col) return;

    // 当前字符不在字典树中
    if (!trie[board[r][c]]) return;

    const temp = board[r][c];
    board[r][c] = "#"; // 标记当前点已经访问过
    dfs(r - 1, c, trie[temp]);
    dfs(r + 1, c, trie[temp]);
    dfs(r, c - 1, trie[temp]);
    dfs(r, c + 1, trie[temp]);
    board[r][c] = temp; // 遍历完当前点的上下左右 4 个点之后恢复现场
  };

  const trie = getTrie(words);
  for (let i = 0; i < row; i++) {
    for (let j = 0; j < col; j++) {
      dfs(i, j, trie);
    }
  }

  return res;
};

电话号码的字母组合

题目地址 (opens new window)

// DFS
var letterCombinations = function(digits) {
  if (!digits.length) return [];
  const res = [];
  const map = {
    "2": "abc",
    "3": "def",
    "4": "ghi",
    "5": "jkl",
    "6": "mno",
    "7": "pqrs",
    "8": "tuv",
    "9": "wxyz"
  };

  const dfs = (cur, i) => {
    // cur 是当前构建的字符串，i 是扫描的指针
    if (i > digits.length - 1) {
      // 指针越界，递归的出口
      res.push(cur); // 将解推入结果中
      return; // 结束当前递归分支，进入另一个递归分支
    }
    const letters = map[digits[i]]; // 当前数字对应哪些字母
    for (const c of letters) {
      // 不同的字母选择代表不同的递归分支
      dfs(cur + c, i + 1); //递归
    }
  };

  dfs("", 0);

  return res;
};

// BFS
var letterCombinations = function(digits) {
  if (!digits.length) return [];
  const queue = [];
  const map = {
    "2": "abc",
    "3": "def",
    "4": "ghi",
    "5": "jkl",
    "6": "mno",
    "7": "pqrs",
    "8": "tuv",
    "9": "wxyz"
  };
  queue.push("");

  for (let i = 0; i < digits.length; i++) {
    // bfs 的层数，即 digits 的长度
    const count = queue.length; // 当前层的节点个数
    for (let j = 0; j < count; j++) {
      const cur = queue.shift(); // 让当前层的节点逐个出队
      const letters = map[digits[i]];
      for (const c of letters) {
        queue.push(cur + c); // 生成新的字母串入列
      }
    }
  }

  return queue; // 队列中全是最后一层生成的字母串
};

位运算

程序中的所有数在计算机内存中都是以二进制的形式存储的。位运算就是直接对整数在内存中的二进制位进行操作。由于位运算直接对内存数据进行操作，不需要转成十进制，因此处理速度非常快。

位运算操作符

符号	描述	运算规则
&	与	两个位都为 1 时，结果才为 1
|	或	两个位都为 0 时，结果才为 0
^	异或	两个位相同为 0，相异为 1
~	取反	0 变 1，1 变 0
<<	左移	各二进位全部左移若干位，高位丢弃，低位补 0
>>	右移	各二进位全部右移若干位，对无符号数，高位补 0，有符号数，各编译器处理方法不一样，有的补符号位（算术右移），有的补 0（逻辑右移）

异或的一些有用特性

x ^ 0 = x;
x ^ 1 = ~x;
x ^ ~x = 1;
x ^ x = 0;
(a ^ b = (c) => (a ^ c = b)), (b ^ c = a);
a ^ b ^ c = a ^ (b ^ c) = a ^ b ^ c;

实战常用的位运算操作

1. 判断奇偶性

x & (1 === 1); // 奇数
x & (1 === 0); // 偶数

这种操作比模运算会更快，因为模运算需要先进行一次除法运算，x % 2 === 1。

2. 清除最低位的 1

x = x & (x - 1);

3. 得到最低位的 1

x & -x;

比较复杂的位运算操作

1. 将 x 最右边的 n 位清零

x & (~0 << n);

2. 获取 x 的第 n 位值（0 或者 1）

(x >> n) & 1;

3. 获取 x 的第 n 位的幂值

x & (1 << (n - 1));

4. 仅将第 n 位置为 1

x | (1 << n);

5. 仅将第 n 位置为 0

x & ~(1 << n);

6. 将 x 的最高位至第 n 位（含）清零

x & ((1 << n) - 1);

7. 将第 n 位至第 0 位（含）清零

x & ~((1 << (n + 1)) - 1);

位 1 的个数

题目地址 (opens new window)

const hammingWeight = (n) => {
  let res = 0;
  for (let i = 0; i < 32; i++) {
    if ((n & (1 << i)) !== 0) {
      res++;
    }
  }
  return res;
};

const hammingWeight = (n) => {
  let res = 0;
  while (n) {
    res++;
    n &= n - 1;
  }
  return res;
};

2 的幂

题目地址 (opens new window)

const isPowerOfTwo = (n) => {
  return n > 0 && (n & (n - 1)) === 0;
};

const isPowerOfTwo = (n) => {
  return n > 0 && (n & -n) === n;
};

const isPowerOfTwo = (n) => {
  if (n < 1) return false;
  while (n !== 1) {
    if (n % 2 === 1) return false;
    n /= 2;
  }
  return true;
};

比特位计数

题目地址 (opens new window)

const countOnes = (x) => {
  let count = 0;
  while (x) {
    count++;
    x &= x - 1;
  }
  return count;
};
const countBits = (n) => {
  const arr = [];
  for (let i = 0; i <= n; i++) {
    arr.push(countOnes(i));
  }
  return arr;
};

const countBits = (n) => {
  const bits = new Array(n + 1).fill(0);
  for (let i = 1; i <= n; i++) {
    bits[i] = bits[i & (i - 1)] + 1;
  }
  return bits;
};

双指针和滑动窗口

合并两个有序数组

题目地址 (opens new window)

// 正向双指针，每次从两个数组头部取出比较小的数字放到结果中
var merge = function(nums1, m, nums2, n) {
  let p1 = 0,
    p2 = 0;
  const sorted = new Array(m + n).fill(0);
  let cur;
  while (p1 < m || p2 < n) {
    if (p1 === m) {
      cur = nums2[p2++];
    } else if (p2 === n) {
      cur = nums1[p1++];
    } else if (nums1[p1] < nums2[p2]) {
      cur = nums1[p1++];
    } else {
      cur = nums2[p2++];
    }
    sorted[p1 + p2 - 1] = cur;
  }
  for (let i = 0; i < m + n; i++) {
    nums1[i] = sorted[i];
  }
};

// 逆向双指针，指针从后向前遍历，每次取两者间较大值放在 nums1 后面
var merge = function(nums1, m, nums2, n) {
  let p1 = m - 1,
    p2 = n - 1;
  let tail = m + n - 1;
  let cur;
  while (p1 >= 0 || p2 >= 0) {
    if (p1 === -1) {
      cur = nums2[p2--];
    } else if (p2 === -1) {
      cur = nums1[p1--];
    } else if (nums1[p1] > nums2[p2]) {
      cur = nums1[p1--];
    } else {
      cur = nums2[p2--];
    }
    nums1[tail--] = cur;
  }
};

有序数组的平方

题目地址 (opens new window)

var sortedSquares = function(nums) {
  let i = 0,
    j = nums.length - 1,
    k = nums.length - 1,
    res = [];
  while (k >= 0) {
    const left = nums[i] ** 2,
      right = nums[j] ** 2;
    if (left < right) {
      res[k] = right;
      j--;
    } else {
      res[k] = left;
      i++;
    }
    k--;
  }
  return res;
};

颜色分类

题目地址 (opens new window)

var sortColors = function(nums) {
  let left = 0,
    right = nums.length - 1,
    cur = 0;
  while (cur <= right) {
    if (nums[cur] === 0) {
      // 0 往前放
      [nums[left], nums[cur]] = [nums[cur], nums[left]];
      left++;
      cur++;
    } else if (nums[cur] === 1) {
      // 1 在原位置不动
      cur++;
    } else if (nums[cur] === 2) {
      // 2 往后放
      [nums[cur], nums[right]] = [nums[right], nums[cur]];
      right--;
    }
  }
};

分发饼干

题目地址 (opens new window)

var findContentChildren = function(g, s) {
  g.sort((a, b) => a - b);
  s.sort((a, b) => a - b);
  let child = 0,
    cookie = 0;
  while (child < g.length && cookie < s.length) {
    if (g[child] <= s[cookie]) {
      child++;
    }
    cookie++;
  }
  return child;
};

验证回文串

题目地址 (opens new window)

var isPalindrome = function(s) {
  s = s.replace(/[^a-zA-Z0-9]/g, "").toLowerCase();
  let l = 0,
    r = s.length - 1;
  while (l < r) {
    if (s[l] !== s[r]) {
      return false;
    }
    l++;
    r--;
  }
  return true;
};

回文子串

题目地址 (opens new window)

// 枚举出所有的子串，然后再判断这些子串是否是回文
var countSubstrings = function(s) {
  let res = 0;
  for (let i = 0; i < s.length; i++) {
    for (let j = i + 1; j <= s.length; j++) {
      if (isPalindrome(s.substring(i, j))) res++;
    }
  }
  return res;
};

function isPalindrome(s) {
  let i = 0,
    j = s.length - 1;
  while (i < j) {
    if (s[i] !== s[j]) return false;
    i++;
    j--;
  }
  return true;
}

// 枚举每一个可能的回文中心，然后用两个指针分别向左右两边拓展，当两个指针指向的元素相同的时候就拓展，否则停止拓展
var countSubstrings = function(s) {
  let res = 0;
  for (let i = 0; i < s.length; i++) {
    res += countPalindrome(s, i, i);
    res += countPalindrome(s, i, i + 1);
  }
  return res;
};

function countPalindrome(s, i, j) {
  let num = 0;
  while (i >= 0 && j < s.length && s[i] === s[j]) {
    num++;
    i--;
    j++;
  }
  return num;
}

最长回文子串

题目地址 (opens new window)

// 中心扩展
var longestPalindrome = function(s) {
  const n = s.length;
  if (n < 2) {
    return s;
  }
  let res = "";
  for (let i = 0; i < n; i++) {
    // 回文子串长度是奇数
    helper(i, i);
    // 回文子串长度是偶数
    helper(i, i + 1);
  }

  function helper(l, r) {
    while (l >= 0 && r < n && s[l] === s[r]) {
      l--;
      r++;
    }
    // 此时 l 到 r 的距离为 r-l+1，但是 l，r 两个边界不能取，所以应该取 l+1 到 r-1 的区间，长度为 (r-1)-(l+1)+1 = r-l-1
    if (r - l - 1 > res.length) {
      // 取 [l+1, r-1] 这个区间的长度
      res = s.slice(l + 1, r);
    }
  }

  return res;
};

三数之和

题目地址 (opens new window)

方法一：两层循环 + set。时间复杂度为：O(n^2)，空间复杂度为：O(n)。

方法二：排序 + 双指针。时间复杂度为：O(n^2)，空间复杂度为：O(1)。

var threeSum = function(nums) {
  const len = nums.length;
  const res = [];

  nums.sort((a, b) => a - b);
  for (let i = 0; i < len; i++) {
    if (nums[i] > 0) break; // 如果当前数字大于 0，那么三数之和一定大于 0，结束循环
    if (i > 0 && nums[i - 1] === nums[i]) continue; // 去重
    let l = i + 1,
      r = len - 1; // l、r 分别指向 i 后面元素的两端
    while (l < r) {
      const sum = nums[i] + nums[l] + nums[r];
      if (sum === 0) {
        res.push([nums[i], nums[l], nums[r]]);
        while (nums[l] === nums[l + 1]) l++; // 去重
        while (nums[r] === nums[r - 1]) r--; // 去重
        l++;
        r--;
      } else if (sum < 0) {
        l++;
      } else {
        r--;
      }
    }
  }

  return res;
};

盛最多水的容器

题目地址 (opens new window)

var maxArea = function(height) {
  let l = 0,
    r = height.length - 1,
    res = 0;

  while (l < r) {
    // 每次移动较小的指针
    if (height[l] < height[r]) {
      res = Math.max(res, (r - l) * height[l]);
      l++;
    } else {
      res = Math.max(res, (r - l) * height[r]);
      r--;
    }
  }

  return res;
};

长度最小的子数组

题目地址 (opens new window)

var minSubArrayLen = function(target, nums) {
  const len = nums.length;
  let left = 0,
    sum = 0,
    res = len + 1;
  for (let right = 0; right < len; right++) {
    sum += nums[right];
    while (sum >= target) {
      res = Math.min(res, right - left + 1);
      sum -= nums[left];
      left++;
    }
  }
  return res > len ? 0 : res;
};

无重复字符的最长子串

题目地址 (opens new window)

var lengthOfLongestSubstring = function(s) {
  const set = new Set();
  let i = 0,
    j = 0,
    max = 0;
  while (j < s.length) {
    if (!set.has(s[j])) {
      set.add(s[j++]);
      max = Math.max(max, set.size);
    } else {
      set.delete(s[i++]);
    }
  }
  return max;
};

最小覆盖子串

题目地址 (opens new window)

// 时间复杂度是：O(m+n)，空间复杂度是：O(m)
var minWindow = function(s, t) {
  const obj = {};
  for (const c of t) {
    obj[c] = obj[c] ? obj[c] + 1 : 1;
  }
  let left = 0,
    right = 0;
  let count = Object.keys(obj).length;
  let minLen = Infinity,
    minStart = 0; // 最小子串的长度和起始位置
  while (right < s.length) {
    const c = s[right++];
    if (obj[c] !== undefined) {
      obj[c]--;
      if (obj[c] === 0) {
        count--;
      }
    }
    while (count === 0) {
      if (right - left < minLen) {
        minLen = right - left;
        minStart = left;
      }
      const c = s[left++];
      if (obj[c] !== undefined) {
        obj[c]++;
        if (obj[c] > 0) {
          count++;
        }
      }
    }
  }
  return minLen === Infinity ? "" : s.substring(minStart, minStart + minLen);
};

替换后的最长重复字符

题目地址 (opens new window)

枚举字符串中的每一个位置作为右端点，然后找到其最远的左端点的位置，满足该区间内除了出现次数最多的那一类字符之外，剩余的字符（即非最长重复字符）数量不超过 k 个。

使用双指针维护这些区间，每次右指针右移，如果区间仍然满足条件，那么左指针不移动，否则左指针至多右移一格，保证区间长度不减小。

虽然这样的操作会导致部分区间不符合条件，即该区间内非最长重复字符超过了 k 个。但是这样的区间也同样不可能对答案产生贡献。当我们右指针移动到尽头，左右指针对应的区间的长度必然对应一个长度最大的符合条件的区间。

由于字符串中仅包含大写字母，我们可以使用一个长度为 26 的数组维护每一个字符的出现次数。每次区间右移，我们更新右移位置的字符出现的次数，然后尝试用它更新重复字符出现次数的历史最大值，最后我们使用该最大值计算出区间内非最长重复字符的数量，以此判断左指针是否需要右移即可。

var characterReplacement = function(s, k) {
  const n = s.length;
  const arr = new Array(26).fill(0);
  const baseCharCode = "A".charCodeAt();
  let max = 0, // 区间内出现次数最多的字符的最大次数
    left = 0,
    right = 0;

  while (right < n) {
    arr[s[right].charCodeAt() - baseCharCode]++;
    max = Math.max(max, arr[s[right].charCodeAt() - baseCharCode]);
    if (right - left + 1 - max > k) {
      // 除了出现次数最多的字符之外，剩余的字符数量如果超过 k 个，就需要移动左指针
      arr[s[left].charCodeAt() - baseCharCode]--;
      left++;
    }
    right++;
  }

  return right - left;
};

找到字符串中所有字母异位词

题目地址 (opens new window)

因为字符串 p 的异位词的长度一定与字符串 p 的长度相同，所以我们可以在字符串 s 中构造一个长度为与字符串 p 的长度相同的滑动窗口，并在滑动中维护窗口中每种字母的数量；当窗口中每种字母的数量与字符串 p 中每种字母的数量相同时，则说明当前窗口为字符串 p 的异位词。

var findAnagrams = function(s, p) {
  const sLen = s.length,
    pLen = p.length;

  if (sLen < pLen) {
    return [];
  }

  const res = [];
  const sCount = new Array(26).fill(0);
  const pCount = new Array(26).fill(0);
  const baseCharCode = "a".charCodeAt();

  for (let i = 0; i < pLen; i++) {
    sCount[s[i].charCodeAt() - baseCharCode]++;
    pCount[p[i].charCodeAt() - baseCharCode]++;
  }

  if (sCount.toString() === pCount.toString()) {
    res.push(0);
  }

  for (let i = 0; i < sLen - pLen; i++) {
    // 移动窗口，注意保持窗口大小不变
    sCount[s[i].charCodeAt() - baseCharCode]--;
    sCount[s[i + pLen].charCodeAt() - baseCharCode]++;

    if (sCount.toString() === pCount.toString()) {
      res.push(i + 1);
    }
  }

  return res;
};

单调栈

每日温度

题目地址 (opens new window)

// 维护一个存储下标的单调栈，从栈底到栈顶的下标对应的温度列表中的温度依次递减
// 如果一个下标在单调栈里，则表示尚未找到下一次温度更高的下标
// 由于单调栈满足从栈底到栈顶元素对应的温度递减，因此每次有元素进栈时，会将温度更低的元素全部移除，并更新出栈元素对应的等待天数，这样可以确保等待天数一定是最小的
var dailyTemperatures = function(temperatures) {
  const len = temperatures.length;
  const stack = [];
  const res = new Array(len).fill(0);
  for (let i = 0; i < len; i++) {
    while (
      stack.length !== 0 &&
      temperatures[i] > temperatures[stack[stack.length - 1]]
    ) {
      const stackTop = stack[stack.length - 1];
      stack.pop();
      res[stackTop] = i - stackTop;
    }
    stack.push(i);
  }
  return res;
};

排序

合并区间

题目地址 (opens new window)

var merge = function(intervals) {
  const res = [];
  intervals.sort((a, b) => a[0] - b[0]); // 先将所有区间按区间左端点进行升序排序
  res.push(intervals[0]);
  for (let i = 0; i < intervals.length; i++) {
    const len = res.length;
    if (intervals[i][0] > res[len - 1][1]) {
      // 如果当前区间的左端点大于结果数组中最后一个区间的右端点，则不需要合并
      res.push(intervals[i]);
    } else {
      if (intervals[i][1] > res[len - 1][1]) {
        // 如果当前区间的右端点大于结果数组中最后一个区间的右端点，则将后者置为前者
        res[len - 1][1] = intervals[i][1];
      }
    }
  }
  return res;
};

无重叠区间

题目地址 (opens new window)

var eraseOverlapIntervals = function(intervals) {
  intervals.sort((a, b) => a[1] - b[1]); // 先将所有区间按区间右端点进行升序排序
  const len = intervals.length;
  let count = 1;
  let right = intervals[0][1]; // 实时维护上一个选择区间的右端点
  for (let i = 0; i < len; i++) {
    if (intervals[i][0] >= right) {
      // 如果当前遍历到的区间与上一区间不重合，就可以贪心地选择这个区间，并更新 right
      count++;
      right = intervals[i][1];
    }
  }
  return len - count;
};

前缀和

除自身以外数组的乘积

题目地址 (opens new window)

var productExceptSelf = function(nums) {
  const len = nums.length;
  // l 和 r 分别表示左右两侧的乘积列表
  const l = new Array(len).fill(0);
  const r = new Array(len).fill(0);
  const res = new Array(len).fill(0);

  // l[i] 为索引 i 左侧所有元素的乘积
  // 对于索引为 0 的元素，因为左侧没有元素，所以 l[0] = 1
  l[0] = 1;
  for (let i = 1; i < len; i++) {
    l[i] = nums[i - 1] * l[i - 1];
  }

  // r[i] 为索引 i 右侧所有元素的乘积
  // 对于索引为 len - 1 的元素，因为右侧没有元素，所以 r[len - 1] = 1
  r[len - 1] = 1;
  for (let i = len - 2; i >= 0; i--) {
    r[i] = nums[i + 1] * r[i + 1];
  }

  // 对于索引 i，除 nums[i] 之外其余各元素的乘积就是左侧所有元素的乘积乘以右侧所有元素的乘积
  for (let i = 0; i < len; i++) {
    res[i] = l[i] * r[i];
  }

  return res;
};

// 空间复杂度为 O(1) 的方法
var productExceptSelf = function(nums) {
  const len = nums.length;
  const res = new Array(len).fill(0);

  // res[i] 表示索引 i 左侧所有元素的乘积
  res[0] = 1;
  for (let i = 1; i < len; i++) {
    res[i] = nums[i - 1] * res[i - 1];
  }

  // r 表示索引 i 右侧所有元素的乘积
  let r = 1;
  for (let i = len - 1; i >= 0; i--) {
    // 对于索引 i，左边的乘积为 res[i]，右边的乘积为 r
    res[i] = res[i] * r;
    // r 需要包含右边所有的乘积，所以计算下一个结果时需要将当前值乘到 r 上
    r *= nums[i];
  }

  return res;
};

长度最小的子数组

题目地址 (opens new window)

// 前缀和 + 二分查找
var minSubArrayLen = function(target, nums) {
  const len = nums.length;
  let res = 0;
  let prefix = new Array(len).fill(0); // 前缀和
  prefix[0] = nums[0];
  for (let i = 1; i < len; i++) {
    prefix[i] = prefix[i - 1] + nums[i];
  }
  for (let i = 0; i < len; i++) {
    // 二分查找
    let left = i,
      right = len - 1;
    while (left <= right) {
      const mid = left + ((right - left) >> 1);
      const temp = i > 0 ? prefix[i - 1] : 0;
      const sum = prefix[mid] - temp;
      if (sum >= target) {
        res = res === 0 ? mid - i + 1 : Math.min(res, mid - i + 1);
        right = mid - 1;
      } else {
        left = mid + 1;
      }
    }
  }
  return res;
};

LRU Cache

• 最近最少使用算法

• 根据最近使用时间来置换，一般使用双向链表来实现

• 查询：O(1)，注意这里是查询最前和最后的节点时的时间复杂度，如果是中间节点就不是 O(1) 了

• 修改、更新：O(1)

LRU 缓存

题目地址 (opens new window)

var LRUCache = function(capacity) {
  this.map = new Map();
  this.capacity = capacity;
};

LRUCache.prototype.get = function(key) {
  if (!this.map.has(key)) {
    return -1;
  }
  const value = this.map.get(key);
  this.map.delete(key);
  this.map.set(key, value);
  return value;
};

LRUCache.prototype.put = function(key, value) {
  if (this.map.has(key)) {
    this.map.delete(key);
  }
  this.map.set(key, value);
  if (this.map.size > this.capacity) {
    this.map.delete(this.map.keys().next().value);
  }
};

LFU Cache

• 最近最不常使用算法

• 先考虑最近使用时间，再根据使用频次来置换

布隆过滤器

• ⼀个很⻓的⼆进制向量和⼀系列随机映射函数。

• 布隆过滤器（Bloom Filter）可以⽤于检索⼀个元素是否在⼀个集合中。如果检索到该元素不在集合中，那么是百分百正确的；如果检索到该元素在集合中，那么有一定的概率是误判。

• 它的优点是空间效率和查询时间都远远超过⼀般的算法，缺点是有⼀定的误识别率和删除困难。

• 应用：比特币、分布式系统。

x、y、z 是事先插入到二进制向量中的，它们会把对应的位置置为 1，而 w 是来查询是否在这个集合中的，只要 w 对应的向量中的位有为 0 的，就说明它不在集合中。

A、E 是事先插入到二进制向量中的，虽然 B 在二进制向量中对应的位都为 1，但实际上并没有这个值，所以此时判断 B 在集合中就属于误判。